usbsr: Sector bounded and slope restricted nonlinearities

The class usbsr is defined by diagonally repeated sector-bounded and slope-restricted nonlinearities of the form

$p=\Delta(q)=\left(\begin{array}{c}\delta(q_1)\\ \vdots\\ \delta(q_N)\end{array}\right),\ \ \ \ q=\left(\begin{array}{c}q_1\\ \vdots\\ q_N\end{array}\right)$

Here

The sector constraint 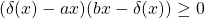$(\delta(x)-ax)(bx-\delta(x))\geq0$ for all $x$ and fixed constants $a\leq0\leq b$
and optionally, the incremental sector constraint (slope restriction)
$c\leq\dfrac{\delta(x_1)-\delta(x_2)}{x_1-x_2}\leq d$
for all $x_1$ , $x_2$ , $x_1\neq x_2$ and with fixed constants $c\leq0\leq d$ .

Note:

$\delta\in slope(c,d)\Rightarrow\delta\in sector(a=c, b=d)$ . Hence, if desired, one can consider tighter sector bounds with $c\leq a$ and $b\leq d$ .
For mathematically more precise formulations of the constraints see [1] and respectively [2] and [23] for the continuous- and discrete time version respectively.

The usbsr class can be defined by

$\Delta_\mathrm{sbsr}=usbsr('name')$
$\Delta_\mathrm{sbsr}=usbsr('name',varargin)$

Just specifying $\Delta_\mathrm{sbsr}=usbsr('name')$ defines a sector bounded nonlinearity, which is repeated once, and which satisfies the constraint $[a,b]=[0,1]$ .

Specifying and/or changing properties proceeds as summarized in the following two tables for properties related to the uncertainty and to IQC-multiplier respectively.

sector\in[a,b] — Uncertainty characteristics

a\leq0\leq b — Uncertainty characteristics

Property	Description
BasisFunctionType	Specify the type of basis function to be used in the multiplier (default = 1). See link for further details.
Length	Specify the length of the basis function (default = 1). See link for further details.
PoleLocation	Specify the pole location of the basis function (default = -1). See link for further details.
SampleTime	Specify the sample time (default = 0).
PrimalDual	Specify whether the multiplier should be a primal/dual parametrization (default = ‘Primal’). – Primal multipliers: ‘Primal’ – Dual multipliers: ‘Dual’ Note: For a standard IQC-analysis, all multipliers must be primal ones.

Multiplier characteristics

Property	Description
NumberOfRepetitions	Specify the number of repetitions of the nonlinearity (default = 1).
SectorBounds	Specify the sector constraints $sector\in[a,b]$ , $a\leq0\leq b$ (default = [0,1]).
SlopeBounds	Specify the slope bounds $slope\in[c,d]$ , $c\leq0\leq d$ (default = [0,0]).
Odd	Specify whether the nonlinearity is Odd (i.e., $f(-x)=-f(x)$ ): – ‘yes‘ – ‘no‘ (default)
InputChannel/ OutputChannel	Specify which input and output channels of the uncertain plant are affected by $\Delta_\mathrm{usbsr}$ . The channels should be specified as: $\begin{array}{c} InputChannel=\left[\! \! \! \begin{array}{ccc}C_{x}^{in}&\cdots&C_{y}^{in}\end{array} \! \! \! \right]\\OutputChannel=\left[ \! \! \! \begin{array}{ccc}C_{v}^{in}&\cdots&C_{w}^{in}\end{array} \! \! \! \right] \end{array}$ Here the order of the channels is not relevant, while $C_{m}^{in}$ , $C_{n}^{out}$ respectively denote the $m^{th}$ and $n^{th}$ in- and output channel of the uncertain plant $M$ .