Sector-bounded and slope-restricted nonlinearities

In this section it is demonstrated how to create a sector-bounded and slope-restricted nonlinearity block. To do so, suppose that this nonlinearity has the following properties:

Name: ‘delta’
Operator type: 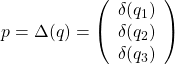, 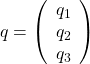is a three times repeated nonlinearity satisfying the constraints:
- Sector constraint: $\delta\in\mathrm{sector}(0,1)$
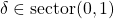
- Slope constraint: $\delta\in\mathrm{slope}(0,1)$
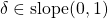
- The nonlinearity is an odd function.
Input channels of 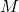$M$ connecting the uncertainty block: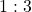 $1:3$
Outputs channels of 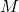$M$ connecting the uncertainty block: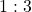 $1:3$

This uncertainty can be created as follows:

delta = iqcdelta('delta','LinNonlin','NL','InputChannel', 1:3,'OutputChannel',1:3,'SectorBounds',[0,1],'SlopeBounds',[0,1],'Odd','yes');

In a next step, you have to assign an IQC-multiplier. The appropriate class for this is called usbsr (for details see here).

Now suppose you want the basis function have the following properties:

Length: 3 (this corresponds to a McMillan degree of 2)
Pole location: -1

This can be specified as:

delta = iqcassign(delta,'usbsr','Length',3, 'PoleLocation',-1);