The file Demo_003.m is found in the IQClab’s folder demos. This demo performs a ![]() – and IQC-robustness analysis for an uncertain plant that is affected by a delay uncertainty. Here it is possible to vary several inputs:
– and IQC-robustness analysis for an uncertain plant that is affected by a delay uncertainty. Here it is possible to vary several inputs:
- xtrIQC
- Use the standard IQC-multiplier, or
- Use an extended one with an additional IQC-constraint
- Performance metric
- Induced
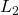 -gain
-gain - Robust stability test
- Induced
The following uncertain plant was taken from [15].
% Define plant
s = tf('s');
G = ss(4/(s^2+0.1*s+1));
Gd = ss(10/(s+0.1));
We = 2/3*ss((s+3.674)^2/(s+0.03)^2);
Wu = ss((s+10)/(s+1e4));
systemnames = 'G Gd';
inputvar = '[p;d;r;u]';
outputvar = '[Gd;r-p-Gd;u;r-p-Gd]';
input_to_G = '[u]';
input_to_Gd = '[G+d]';
cleanupsysic = 'yes';
olic = sysic;
wolic = ssbal(blkdiag(1,We,Wu,1)*olic);
[K,CL,gamma] = hinfsyn(wolic(2:end,2:end),1,1);
M = minreal(lft(wolic,K));
In this demo, we assume that the uncertainty block is defined by the ![]() with
with ![]() and
and ![]() being the maximum time-delay.
being the maximum time-delay.
The demo file Demo_003.m allows to run an IQC-analysis for various values of ![]() and within the file one can change the inputs mentioned above. For illustration purposes, the following 4 lines of code specify an IQC-analysis for the uncertain plant
and within the file one can change the inputs mentioned above. For illustration purposes, the following 4 lines of code specify an IQC-analysis for the uncertain plant ![]() , with
, with ![]() and
and ![]() , and the induced
, and the induced ![]() -gain as performance metric. In addition, the following parameters are considered:
-gain as performance metric. In addition, the following parameters are considered:
- Length of the basis function: 3
- Extra IQC-constraint: ‘yes’
- Solution check: ‘on’
- Enforce strictness of the LMIs:

% M as above
% Define uncertainty block
de = iqcdelta('de','InputChannel',1,'OutputChannel',1, 'StaticDynamic','D','DelayType',1,'DelayTime',0.04);
% Assign IQC-multiplier to uncertainty block
de = iqcassign(de,'udel','Length',3 ,'AddIQC','yes');
% Define performance block
pe = iqcdelta('pe','ChannelClass','P','InputChannel',2, 'OutputChannel',2,'PerfMetric','L2');
% Perform IQC-analysis
prob = iqcanalysis(M,{de,pe},'SolChk','on','eps',1e-8);
If running the IQC analysis in Demo_003.m for
- xtrIQC: ‘No’ (Option 1.1)
- Induced
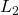 -gain performance (Option 2.1)
-gain performance (Option 2.1)
you obtain the worst-case induced ![]() -gain for increasing values of
-gain for increasing values of ![]() computed by the
computed by the ![]() -tools (command: wcgain) and the IQC-tools for different lengths of the basis function. This yields the results shown in the following. As can be seen, the IQC-analysis produces worst-case induced
-tools (command: wcgain) and the IQC-tools for different lengths of the basis function. This yields the results shown in the following. As can be seen, the IQC-analysis produces worst-case induced ![]() -gains (i.e.,
-gains (i.e., ![]() -norms in this example), which identical to the
-norms in this example), which identical to the ![]() -analysis. In addition, dynamic IQC-multipliers seem not to have an advantage over static ones.
-analysis. In addition, dynamic IQC-multipliers seem not to have an advantage over static ones.
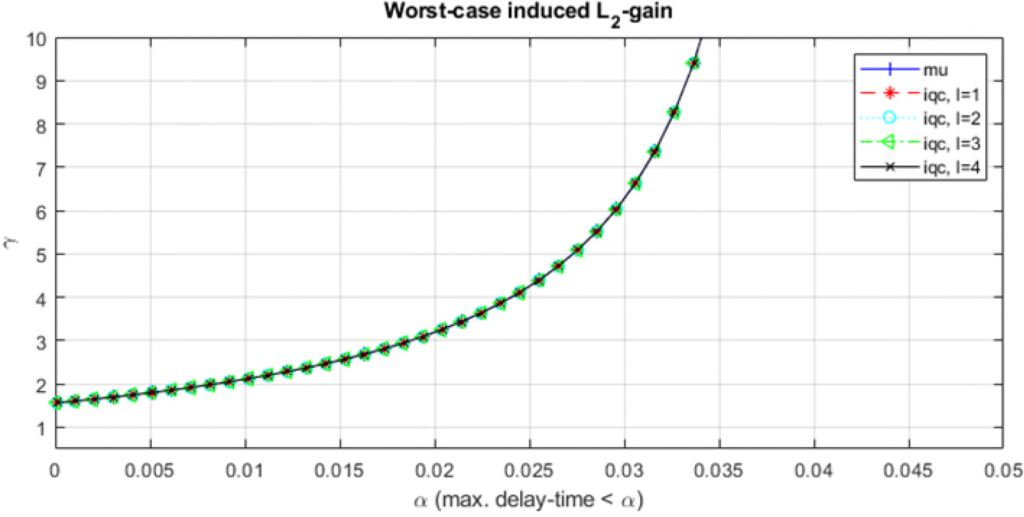
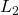 -gain for increasing maximum delay values
-gain for increasing maximum delay values 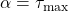 and different lengths of the basis function (scenario: without extra IQC-constraint).
and different lengths of the basis function (scenario: without extra IQC-constraint).For comparison reasons, if running the IQC analysis in Demo_003.m for
- xtrIQC: ‘Yes’ (Option 1.2)
- Induced
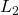 -gain performance (Option 2.1)
-gain performance (Option 2.1)
the IQC-analysis clearly offers an advantage over the ![]() -analysis at the cost of an extra computational load. This can be seen in the following figure.
-analysis at the cost of an extra computational load. This can be seen in the following figure.
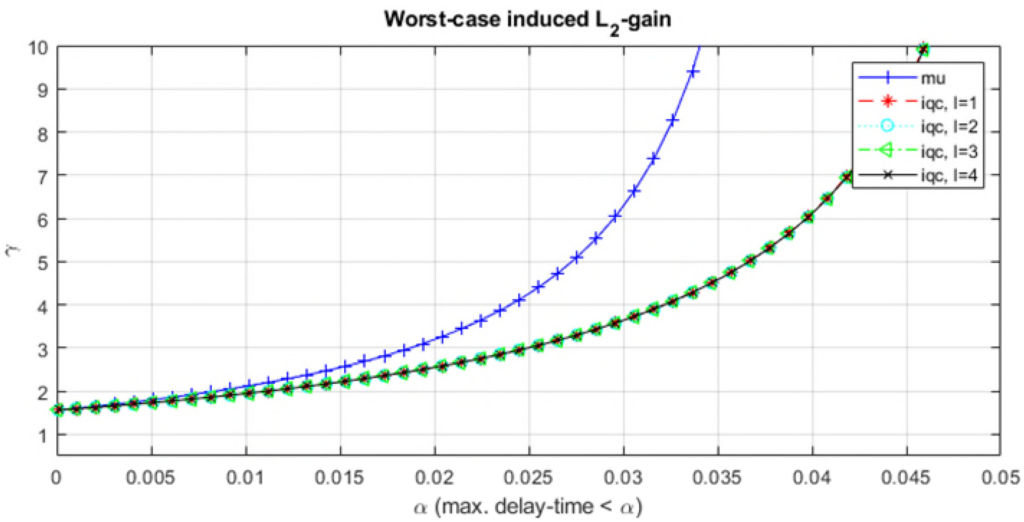
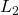 -gain for increasing maximum delay values
-gain for increasing maximum delay values 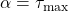 and different lengths of the basis function (scenario: with extra IQC-constraint).
and different lengths of the basis function (scenario: with extra IQC-constraint). 