The file Demo_005.m is found in IQClab’s folder demos. This demo performs an IQC robustness analysis for an uncertain plant that is affected by rate-bounded time-varying parametric uncertainties. Here it is possible to vary several inputs:
- The uncertainty block:
- One rate-bounded parametric uncertainty that is repeated twice, or
- Two rate-bounded parametric uncertainties that are repeated once.
- Relaxation type:
- DG-scalings
- Convex hull relaxation
- Partial convexity
- Zeroth order Polya relaxation
The uncertain system is given by ![]() with the open-loop LTI plant
with the open-loop LTI plant ![]() , where
, where
![]() ,
, ![]() ,
, 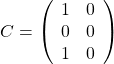 ,
, 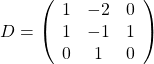 ,
,
On the other hand, the uncertainty block is defined by:
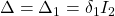 with
with ![Rendered by QuickLaTeX.com \delta_1\in[-0.3,0.3]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-cf45690672766d60449eef724a6d3b04_l3.png?media=1702023987) ,
, ![Rendered by QuickLaTeX.com \dot{\delta}_1\in[-\alpha,\alpha]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-06f85a27487cbac5f4972f3b40d6f2a3_l3.png?media=1702023987) for Option 1.1, or
for Option 1.1, or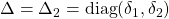 with
with ![Rendered by QuickLaTeX.com \delta_i\in[-0.,0.3]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-9a1b5d9be4dd7d8a7eb46994185e269d_l3.png?media=1702023987) ,
, ![Rendered by QuickLaTeX.com \dot{\delta}_i\in[-\alpha,\alpha]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-e2ef87bc0b14f1b55686846e1bc2e92e_l3.png?media=1702023987) ,
,  for Option 1.2.
for Option 1.2.
The demo file Demo_005.m runs an IQC-analysis for various values of ![]() and within the file you can change the inputs mentioned above. If running the analysis for
and within the file you can change the inputs mentioned above. If running the analysis for ![]() for all available relaxation schemes, we obtain the following results shown in the following figures. As can be seen, the
for all available relaxation schemes, we obtain the following results shown in the following figures. As can be seen, the ![]() -analysis provides a lower-bound, while the IQC analysis with static IQC-multipliers provides an upper-bound on the worst-case induced
-analysis provides a lower-bound, while the IQC analysis with static IQC-multipliers provides an upper-bound on the worst-case induced ![]() -gain. In addition, if increasing the length of the basis function, and thereby introducing dynamics in the IQC multipliers, all the results show an increasing worst-case induced
-gain. In addition, if increasing the length of the basis function, and thereby introducing dynamics in the IQC multipliers, all the results show an increasing worst-case induced ![]() -gain for increasing rate-bounds on the uncertainties. Moreover, if changing the relaxation scheme, one can clearly see the benefit of the Partial concexity and zeroth order Polya relaxation over the convex hull relaxation and the DG-scaling; this at the cost of a higher computational load.
-gain for increasing rate-bounds on the uncertainties. Moreover, if changing the relaxation scheme, one can clearly see the benefit of the Partial concexity and zeroth order Polya relaxation over the convex hull relaxation and the DG-scaling; this at the cost of a higher computational load.
 -gain for increasing rate-bounds
-gain for increasing rate-bounds 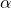 (with DG-scalings relaxation scheme)
(with DG-scalings relaxation scheme)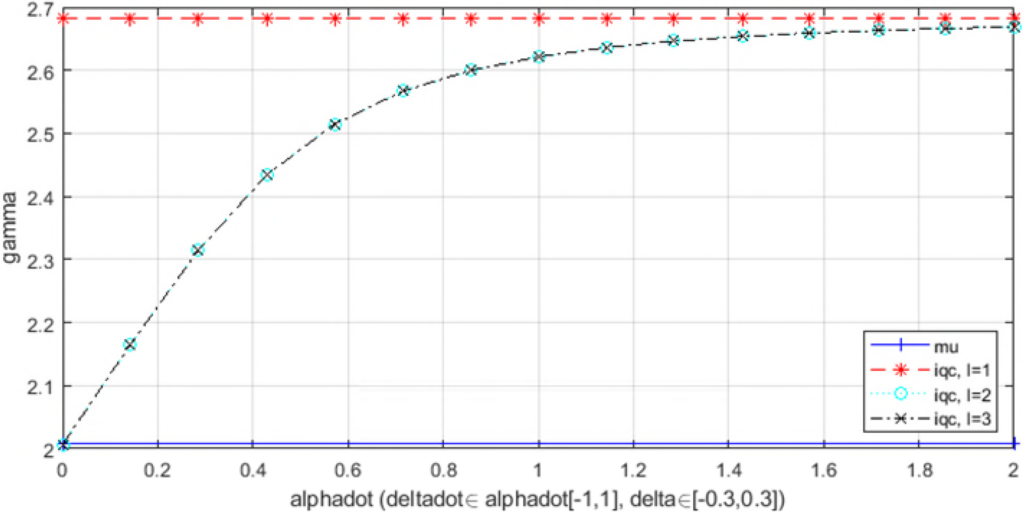
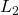 -gain for increasing rate-bounds
-gain for increasing rate-bounds 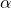 (with the convex hull relaxation scheme)
(with the convex hull relaxation scheme)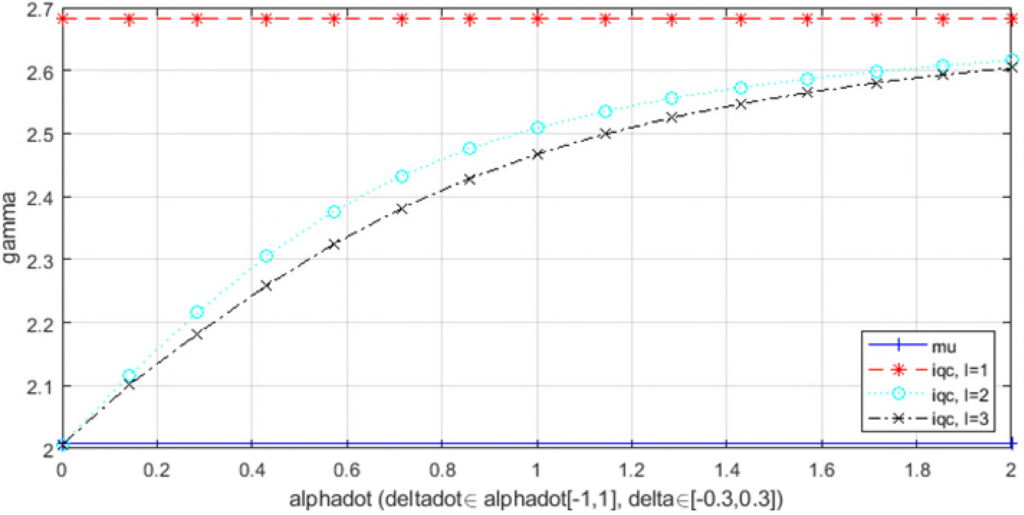
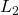 -gain for increasing rate-bounds
-gain for increasing rate-bounds 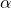 (with the partial convexity relaxation scheme)
(with the partial convexity relaxation scheme)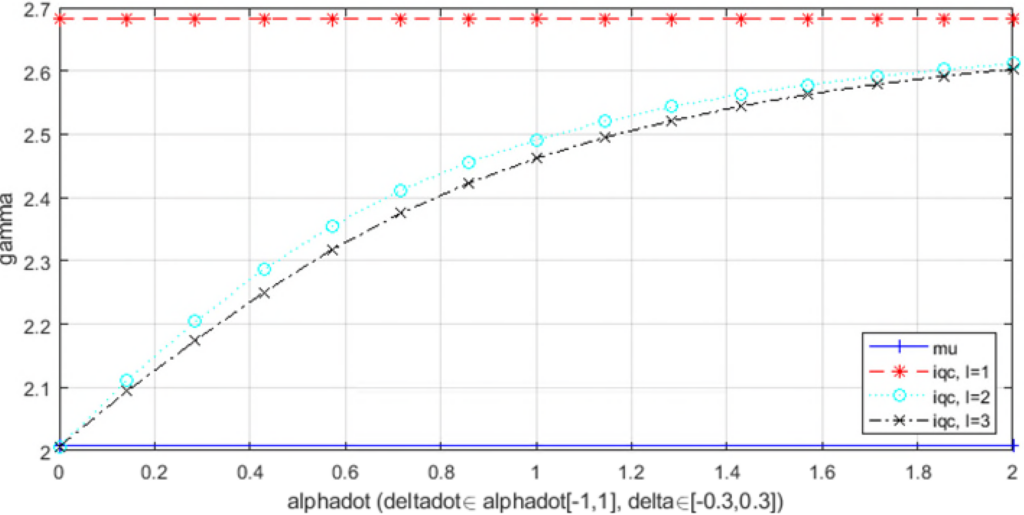
 -gain for increasing rate-bounds
-gain for increasing rate-bounds  (with the zeroth order Polya relaxation scheme)
(with the zeroth order Polya relaxation scheme) 