IQClab offers the possibility to perform ![]() -syntheses. The algorithm is similar to the (LMI-based) one available in the MATLAB Robust Control Toolbox. However, it offers some additional features that are (currently) not available in the Robust Control Toolbox.
-syntheses. The algorithm is similar to the (LMI-based) one available in the MATLAB Robust Control Toolbox. However, it offers some additional features that are (currently) not available in the Robust Control Toolbox.
Note: It is assumed that the user is acquainted with the ![]() -controller synthesis literature and tools. The reader is referred to [3], [4], [5] and references therein for further information.
-controller synthesis literature and tools. The reader is referred to [3], [4], [5] and references therein for further information.
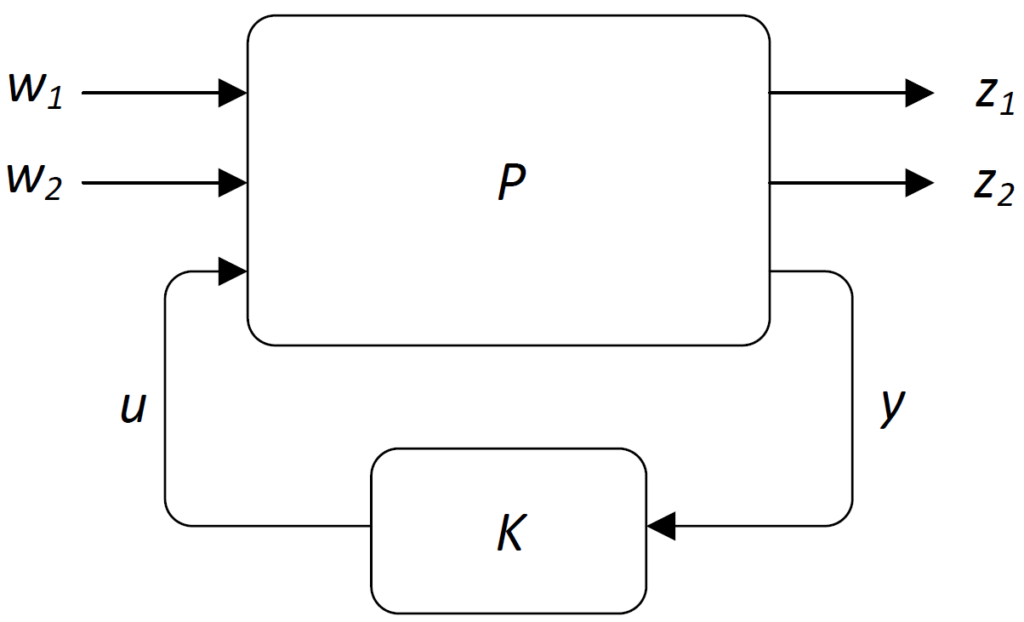
We consider the system interconnection shown in the figure below, where ![]() is the weighted generalized plant (i.e., it is assumed that the disturbance and performance weights are already incorporated in the plant) and where
is the weighted generalized plant (i.e., it is assumed that the disturbance and performance weights are already incorporated in the plant) and where ![]() is the to-be-designed controller. The generalized plant has disturbance inputs
is the to-be-designed controller. The generalized plant has disturbance inputs ![]() and
and ![]() , performance outputs
, performance outputs ![]() and
and ![]() , control input
, control input ![]() , and measurement output
, and measurement output ![]() .
.
Some characteristics of the algorithm are:
- The algorithms performs a synthesis with the aim to obtain a controller,
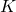 , which stabilizes the plant
, which stabilizes the plant 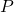 and which renders/minimizes the performance specification on the channels
and which renders/minimizes the performance specification on the channels  and
and 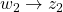 satisfied as detailed next.
satisfied as detailed next. - The algorithm allows to impose the following norm constraints on the performance channels
 and
and 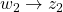 respectively:
respectively:- A fixed norm-bound,
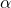 , on the performance channel
, on the performance channel 
.![Rendered by QuickLaTeX.com \[\int_0^{\infty}\left(\begin{array}{c}z_1(t)\\w_1(t)\end{array}\right)^T\left(\begin{array}{cc}\frac{1}{\alpha}I&0\\0&-\alpha I\end{array}\right)\left(\begin{array}{c}z_1(t)\\w_1(t)\end{array}\right)dt\geq0\ \ \forall t\geq0\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-6ce0847601db2c8113ffdd6cb9750304_l3.png?media=1702023987)
- A to-be-minimized norm-bound.
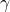 , on the performance channel
, on the performance channel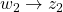
.![Rendered by QuickLaTeX.com \[\int_0^{\infty}\left(\begin{array}{c}z_2(t)\\w_2(t)\end{array}\right)^T\left(\begin{array}{cc}\frac{1}{\gamma}I&0\\0&-\gamma I\end{array}\right)\left(\begin{array}{c}z_2(t)\\w_2(t)\end{array}\right)dt\geq0\ \ \forall t\geq0\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-1a968fa36cddcd2e3f3f3742ea496968_l3.png?media=1702023987)
- A fixed norm-bound,
- In addition, the algorithm can take initial LMI solutions to invoke warm-starts.
Note: The channel ![]() can be included in the synthesis to robustify your control design by imposing the extra norm-constraint (small-gain). Thereby the function allows to include (dynamically weighted) uncertainty channels, which in turn facilitates, for example,
can be included in the synthesis to robustify your control design by imposing the extra norm-constraint (small-gain). Thereby the function allows to include (dynamically weighted) uncertainty channels, which in turn facilitates, for example, ![]() iteration type algorithms based on general dynamic multipliers [6].
iteration type algorithms based on general dynamic multipliers [6].
Usage:
If feasible, the algorithms returns:
- The stabilizing controller

- The
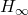 -norm,
-norm, 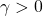 , on the performance channel
, on the performance channel 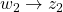 of the closed-loop system
of the closed-loop system 
- The LMI certificate

The inputs should be provided as follows:
- The LTI plant
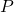 is assumed to admit the following state space description
is assumed to admit the following state space description
where![Rendered by QuickLaTeX.com \[\left(\!\!\!\begin{array}{c}z_1\\z_2\\y\end{array}\!\!\!\right)\!=\!\left[\!\!\begin{array}{c|ccc}A&B_{w_1}&B_{w_2}&B_u\\ \hline C_{z_1}&D_{z_1,w_1}}&D_{z_1,w_2}}&D_{z_1,u}\\C_{z_2}&D_{z_2,w_1}}&D_{z_2,w_2}}&D_{z_2,u}\\C_{y}&D_{y,w_1}}&D_{y,w_2}}&D_{y,u}\end{array}\!\!\right]\!\!\!\left(\!\!\begin{array}{c}w_1\\w_2\\u\end{array}\!\!\!\right),\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-9267824c98891c9d0350eb18047827d4_l3.png?media=1702023987)
 and
and 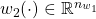 are the (generalized) disturbance inputs
are the (generalized) disturbance inputs and
and 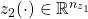 are the performance outputs
are the performance outputs is the control input
is the control input
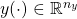 is the measurement output
is the measurement output
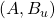 is stabilizable and
is stabilizable and  is detectable
is detectable
- In addition, the plant input and output dimension data
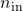 and
and 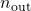 should be specified as follows:
should be specified as follows:![Rendered by QuickLaTeX.com n_\mathrm{in}=[n_{w_1};n_{w_2};n_u]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-d3b31bccbe04140d736ffc2d71b55e36_l3.png?media=1702023987)
![Rendered by QuickLaTeX.com n_\mathrm{out}=[n_{z_1};n_{z_2};n_y]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-fb587ffa0926e4f9aeec4774d56b0ce0_l3.png?media=1702023987)
- Note: In case
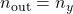 and
and 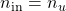 , it is assumed that
, it is assumed that 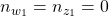 and that the remaining in- and output channels are associated with the second performance channel
and that the remaining in- and output channels are associated with the second performance channel  .
.
- The last input, options, is a structure with various options as summarized in the following table.
| Options | Description |
| options.subopt | If chosen larger than 1, the algorithm computes a suboptimal solution The default value is 1.01. |
| options.condnr | If chosen larger than 1, the algorithm computes a suboptimal solution by maximizing The default value is 1. |
options.uv | Use different options to reconstruct the controller: – options.uv=1 for – options.uv=2 for The default value is 1. |
| options.eliminate | – options.eleminate=1 solves the controller synthesis problem in one shot (i.e. without eliminating the control variable by projection). – options.eleminate=2 employs the elimination lemma to remove the controller variables form the optimization problem, which allows solving an LMI problem with less optimization variables. The default value is 2. |
| options.Lyapext | With this option you can specify how the Lyapunov function matrix The default value is 5. |
| options.constants | options.constants= The constants are associated with the following LMI constraints – – – The default value is |
| options.init | This is a structure with: – options.init. – options.init. This option can be used to specify an initial condition in the corresponding optimization problem. This option only works for options.eliminate=2 and options.balreal=0. The matrices are empty by default. |
| options.controller | In case options.eliminate=2, you can construct the controller in different fashions by specifying: – options.eliminate=1: This options contructs the controller analytically by means of the function fInvproj (see link for further details) – options.eliminate=2: This option constructs the controller by means of solving an LMI problem. The default value is 1. |
| options.alpha | This option specifies the maximum The default value is 1. |
| options.gmax | This option specifies the maximum The default value is 1000. |
| options.balreal | This option pre-processes the open-loop weighted generalized plant in the following sense: – options.balreal=0: No balancing is applied – options.balreal=1: A Grammian based IO balancing is applied – options.balreal=2: An – options.balreal=3: An norm-balancing is applied by means of the command ssbal. This command computes a diagonal similarity transformation The default value is 0. |
| options.Parser | The option options.Parser specifies which parser is used: – options.Parser=’LMIlab’ – options.Parser=’Yalmip’ The default options is ‘LMIlab’. |
| options.Solver | The option options.Solver specifies which solver is used when considering Yalmip as parser. See https://yalmip.github.io/ for further info. The default solver is ‘mincx’. |
| options.FeasbRad | This option allows setting the feasibility radius of the optimization problem (see MATLAB → help → mincx for further details). The default value is 1e6. |
| options.Terminate | This option can be used to change the LMI solver options (see MATLAB → help → mincx for further details). The default value is 0. |
| options.RelAcc | This option can be used to change the LMI solver options (see MATLAB → help → mincx for further details). The default value is 1e-3. |
