IQClab also provides the option to design robust estimators with general dynamic multipliers.
Note: It is assumed that the user is acquainted with the robust estimation literature. The reader is referred to [24] and references therein for further information.
The algorithm considered here corresponds to the one described in [24], which considers the problem of synthesizing robust estimators based on dynamic IQCs. This problem is convex and based on solving an LMI problem.
We consider the system interconnection shown in the following figure.

Here:
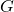 is the plant model
is the plant model is the uncertainty block, which is assumed to have a block diagonal structure
is the uncertainty block, which is assumed to have a block diagonal structure  . The properties of the individual blocks should be compatible with those from the class iqcdelta (see details here)
. The properties of the individual blocks should be compatible with those from the class iqcdelta (see details here) is the to-be-designed robust estimator
is the to-be-designed robust estimator- the in- and output channels are given by
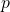 and
and  are the uncertainty in- and outputs
are the uncertainty in- and outputs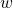 is the disturbance input
is the disturbance input is the to-be-estimated output
is the to-be-estimated output
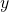 is the measurement output
is the measurement output is the estimation error output
is the estimation error output
Some characteristics of the algorithm are:
- The algorithms solves an LMI problem with the aim to synthesize a robust estimator,
 , which, for all
, which, for all 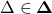 , ensures that the interconnection in the figure above is robustly stable, while the induced
, ensures that the interconnection in the figure above is robustly stable, while the induced 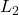 -gain or
-gain or 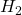 -norm from
-norm from  rendered less than
rendered less than 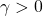 .
. - The
 -block is compatible with the class iqcdelta (see details here)
-block is compatible with the class iqcdelta (see details here)
Usage:
If feasible, the algorithm returns:
- The estimator
 .
. - The (guaranteed) induced
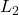 -gain or
-gain or 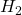 -norm,
-norm, 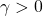 , on the channel
, on the channel  .
.
The inputs should be provided as follows:
- The (stable) LTI plant
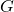 is assumed to admit the following state space description
is assumed to admit the following state space description
where![Rendered by QuickLaTeX.com \[\left(\!\!\!\begin{array}{c}q\\z\\y\end{array}\!\!\!\right)\!=\!\left[\!\!\begin{array}{c|ccc}A&B_\mathrm{p}&B_\mathrm{w}\\ \hline C_\mathrm{q}&D_{\mathrm{qp}}&D_{\mathrm{qw}}\\ C_\mathrm{z}&D_{\mathrm{zp}}&D_{\mathrm{zw}}\\ C_\mathrm{y}&D_{\mathrm{yp}}&D_{\mathrm{yw}} \end{array}\!\!\right]\!\!\!\left(\!\!\begin{array}{c}p\\w\end{array}\!\!\!\right),\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-141ee01d7cbe381664d9b4bc6d7f6668_l3.png?media=1702023987)
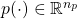 and
and 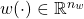 are the uncertainty and disturbance inputs, while
are the uncertainty and disturbance inputs, while 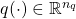 ,
,  , and
, and 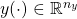 are the uncertainty, to-be-estimated, and measurement outputs respectively.
are the uncertainty, to-be-estimated, and measurement outputs respectively.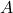 is Hurwitz.
is Hurwitz.- The uncertainty block
 is an iqcdelta object, to which IQC-multipliers have been assigned with iqcassign (see details here).
is an iqcdelta object, to which IQC-multipliers have been assigned with iqcassign (see details here). - The plant input and output dimension data
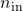 and
and 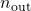 must be specified as follows:
must be specified as follows:
- The last input, options, is a structure with various options as summarized in the following table.
| Options | Description |
| options.perf | Selects the performance metric of interest (i.e., induced – options.perf = ‘L2’ (default) – options.perf = ‘H2’ |
| options.subopt | If chosen larger than 1, the algorithm computes a suboptimal solution The default value is 1.01. |
| options.constants | options.constants= The constants are associated with the following LMI constraints – – – – The default value is |
| options.StrProp | Enforces the estimator, – options.StrProp = ‘no’ (default) – options.StrProp = ‘yes’ |
| options.Parser | The option options.Parser specifies which parser is used: – options.Parser=’LMIlab’ – options.Parser=’Yalmip’ The default options is ‘LMIlab’. |
| options.Solver | The option options.Solver specifies which solver is used when considering Yalmip as parser. See https://yalmip.github.io/ for further info. The default solver is ‘mincx’. |
| options.FeasbRad | This option allows setting the feasibility radius of the optimization problem (see MATLAB → help → mincx for further details). The default value is 1e9. |
| options.Terminate | This option can be used to change the LMI solver options (see MATLAB → help → mincx for further details). The default value is 0. |
| options.RelAcc | This option can be used to change the LMI solver options (see MATLAB → help → mincx for further details). The default value is 1e-4. |
