The file Demo_001.m is found in IQClab’s folder demos. This demo performs a ![]() – and IQC-robustness analysis for an uncertain plant that is affected by LTI parametric uncertainties. Here it is possible to vary several inputs:
– and IQC-robustness analysis for an uncertain plant that is affected by LTI parametric uncertainties. Here it is possible to vary several inputs:
- The uncertainty block:
- One parametric uncertainty that is repeated twice, or
- Two different parametric uncertainties that are repeated once
- Relaxation type:
- DG-scalings
- Convex hull relaxation
- Partial convexity
- Zeroth order Poyla relaxation
- Performance metric:
- Induced
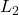 -gain
-gain 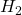 -norm
-norm- Robust stability test
- Induced
The uncertain system is given by ![]() with the open-loop LTI plant
with the open-loop LTI plant ![]() , where
, where
![]() ,
, ![]() ,
, 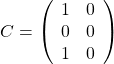 ,
,  ,
,
while:
 for Option 3.1 and Option 3.3,
for Option 3.1 and Option 3.3, for Option 3.2.
for Option 3.2.
On the other hand, the uncertainty block is defined by:
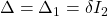 with
with ![Rendered by QuickLaTeX.com \delta\in[-\alpha,\alpha]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-49eeea6b9eebbcccb36d25891259fa81_l3.png?media=1702023987) , for Option 1.1, or
, for Option 1.1, or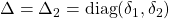 with
with ![Rendered by QuickLaTeX.com \delta_1\in[-\alpha_1,\alpha_1]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-024892574aca1a7ad232bb945e7f6350_l3.png?media=1702023987) ,
, ![Rendered by QuickLaTeX.com \delta_2\in[-\alpha_2,\alpha_2]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-edb661902d1ba00026f1762d02389002_l3.png?media=1702023987) for Option 1.2.
for Option 1.2.
The demo file Demo_001.m allows to run an IQC-analysis for various values of ![]() and within the file one can change the inputs mentioned above. For illustration purposes, the following 5 lines of code specify an IQC-analysis for the uncertain plant
and within the file one can change the inputs mentioned above. For illustration purposes, the following 5 lines of code specify an IQC-analysis for the uncertain plant ![]() ,
, ![]() for
for ![]() and the induced
and the induced ![]() -gain as performance metric. In addition, the following parameters are considered:
-gain as performance metric. In addition, the following parameters are considered:
- Relaxation type: ‘CH’ (Option 2.2)
- Length of the basis function: 2
- Solution check: ‘on’
- Enforce strictness of the LMIs:

% Define uncertain plant
M = ss([-2,-3;1,1],[1,0,1;0,0,0],[1,0;0,0;1,0],[1,-2,0;1,-1,1;0,1,0]);
% Define uncertainty block
de = iqcdelta('de','InputChannel',1:2,'OutputChannel',1:2,'Bounds',[-0.5,0.5]);
% Assign IQC-multiplier to uncertainty block
de = iqcassign(de,'ultis','Length',3,'RelaxationType','CH');
% Define performance block
pe = iqcdelta('pe','ChannelClass','P','InputChannel',3, 'OutputChannel',3,'PerfMetric','L2');
% Perform IQC-analysis
prob = iqcanalysis(M,{de,pe},'SolChk','on','eps',1e-8);
To continue, if running the IQC analysis in Demo_001.m for
 (Option 1.1)
(Option 1.1)- Convex hull relaxation (Option 2.2)
- Induced
 -gain performance (Option 3.1)
-gain performance (Option 3.1)
you obtain as output the worst-case induced ![]() -gain for increasing values of
-gain for increasing values of ![]() computed by the
computed by the ![]() -tools (command: wcgain) and the IQC-tools for different lengths of the basis function. This yields the results shown in the following figure. As can be seen, the IQC-analysis produces worst-case induced
-tools (command: wcgain) and the IQC-tools for different lengths of the basis function. This yields the results shown in the following figure. As can be seen, the IQC-analysis produces worst-case induced ![]() -gains (i.e.
-gains (i.e. ![]() -norms in this example), which are consisted with the
-norms in this example), which are consisted with the ![]() -analysis. For static multipliers (case:
-analysis. For static multipliers (case: ![]() , red dashed-line) the
, red dashed-line) the ![]() -level increases faster than the others, at the benefit of a lower computational load. On the other hand, for basis-lengths larger than
-level increases faster than the others, at the benefit of a lower computational load. On the other hand, for basis-lengths larger than ![]() , the results coincide the
, the results coincide the ![]() -analysis up to values of
-analysis up to values of ![]() . Choosing higher basis-lengths would allow to converge even further.
. Choosing higher basis-lengths would allow to converge even further.
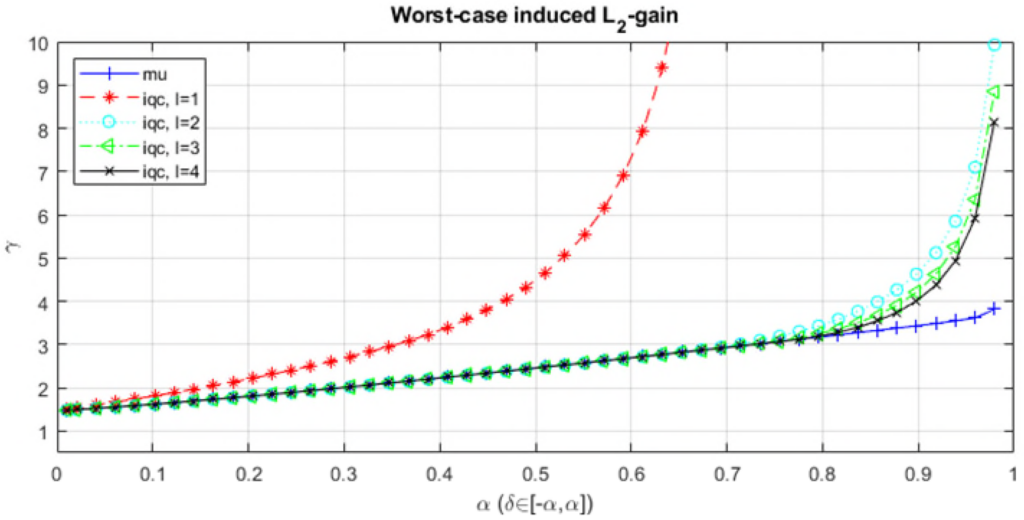
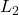 -gain for increasing values of
-gain for increasing values of 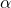 and different lengths of the basis function
and different lengths of the basis function