The first model order reduction tool is a balanced truncation algorithm that allows performing model order reductions for stable continuous-time LTI systems. This proceeds as follows:
The function ![]() fMOR
fMOR![]() performs a model (i.e., state reduction) on the stable MIMO system
performs a model (i.e., state reduction) on the stable MIMO system ![]() .
.
Here the inputs, if specified, denote:
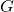 is the model
is the model is a frequency vector (covering the design frequency range for plotting (e.g.,
is a frequency vector (covering the design frequency range for plotting (e.g., 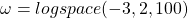 )
)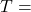 ‘name’ is the title of the figure
‘name’ is the title of the figure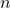 is the desired state dimension of the reduced system
is the desired state dimension of the reduced system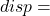 ‘off’ turns off the graphical interface
‘off’ turns off the graphical interface
Note: If ![]() is chosen as
is chosen as ![]() , the system only removes uncontrollable and unobservable states with a tolerance of (i.e., the Hankel singular values with a magnitude of)
, the system only removes uncontrollable and unobservable states with a tolerance of (i.e., the Hankel singular values with a magnitude of) ![]() .
.
As output, you obtain the reduced system ![]() .
.
Example
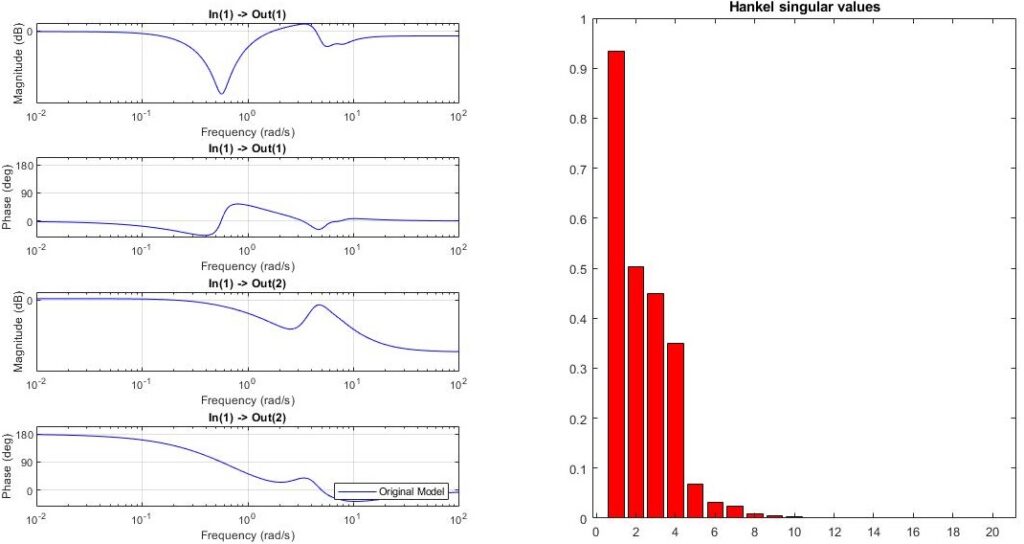
The following code generates a random ![]() state space model with
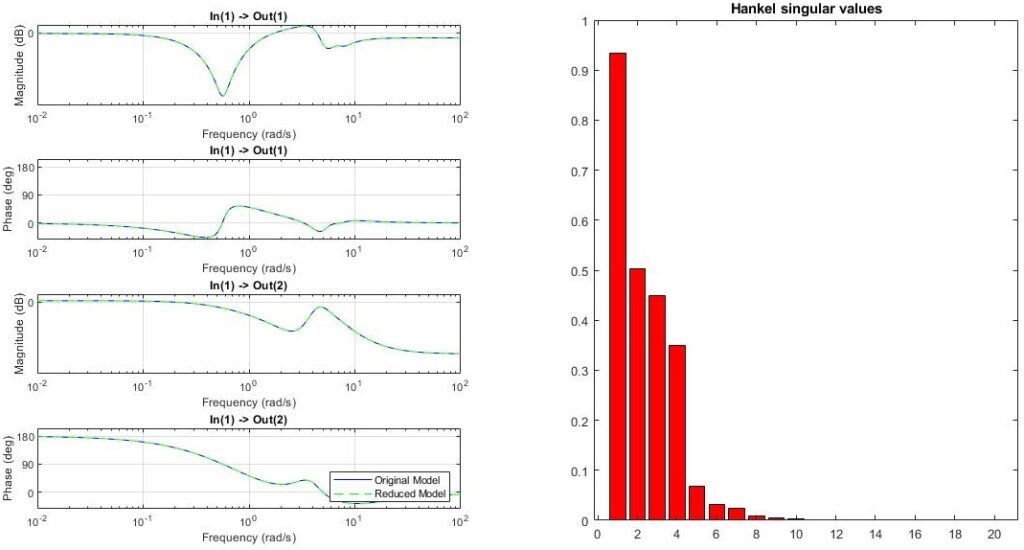
state space model with ![]() states. The function then plots the Bode plots together with the Hankel singular values as shown in the figure. Subsequently, the user is asked to specify the model order, after which the Bode plots of the reduced order model are plotted in the same figure as shown below. This allows to directly assess the quality of the reduced order model (in terms of Bode diagrams).
states. The function then plots the Bode plots together with the Hankel singular values as shown in the figure. Subsequently, the user is asked to specify the model order, after which the Bode plots of the reduced order model are plotted in the same figure as shown below. This allows to directly assess the quality of the reduced order model (in terms of Bode diagrams).
G = rss(20,2,1);
w = logspace(-2,2,1000);
Gred = fMOR(G,w)