Delay uncertainties

In this section it is demonstrated how to create a delay uncertainty block. To do so, suppose that this uncertainty has the following properties:

name: ‘del’
type of operator: $\Delta_\mathrm{del}=(e^{-s\tau}-1)I_{nr}$
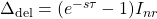
delay time: $\tau=0.1$
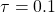
number of repetitions: $nr=3$
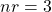
Input channels of connecting the uncertainty block: 1:3
Outputs channels of connecting the uncertainty block: 1:3

This uncertainty can be created as follows:

del = iqcdelta('del','StaticDynamic','D','InputChannel', 1:3,'OutputChannel',1:3,'DelayTime',0.1);

In a next step, you have to assign an IQC-multiplier. The appropriate class for this is called udel (for details see here).

Now suppose you want the basis function have the following properties:

Length: 3 (this corresponds to a McMillan degree of 2)
Pole location: -1

This can be specified as:

del = iqcassign(del,'udel','Length',3, 'PoleLocation',-1);

Note: There is an optional IQC-constraint for this type of delay uncertainties that is added by default. If you wish to turn this optional constraint off (to reduce the computational load, but at the cost of performance), then should can specify:

del = iqcassign(del,'udel','Length',3, 'PoleLocation',-1,'AddIQC','off');