It frequently happens that one would like to implement control-switching schemes to facilitate changing modes, where different controller are subsequently active with the aim to achieve different objectives. Many of such control implementations can be subsumed as shown in the following interconnection.
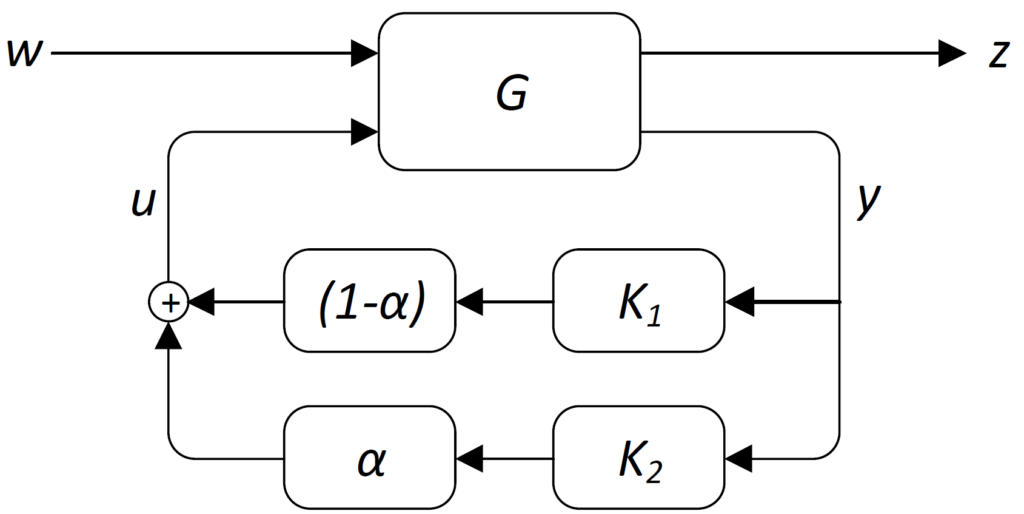
Here ![]() is the plant to be controlled, while
is the plant to be controlled, while ![]() ,
, ![]() , represents the control switching scheme (i.e. for
, represents the control switching scheme (i.e. for ![]() controller
controller ![]() is active, while for
is active, while for ![]() controller
controller ![]() is active). Here
is active). Here ![]() is a time-varying parameter that in practice is often switched from 0 to 1 in an instantaneous manner. In other more careful implementations, the parameter
is a time-varying parameter that in practice is often switched from 0 to 1 in an instantaneous manner. In other more careful implementations, the parameter ![]() is slowly varied for 0 to 1 to facilitate a smoother transitioning between the different controllers.
is slowly varied for 0 to 1 to facilitate a smoother transitioning between the different controllers.
There are a few issues with this approach:
- An instantaneous switch may cause significant disruptions in the closed loop system. The effect is similar to recovering from a nonzero initial condition.
- For smoother implementations, where
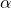 is varied slowly from 0 to 1, it is unknown if the closed loop system is guaranteed to be stable. This is certainly a problem if either one of the controllers is unstable.
is varied slowly from 0 to 1, it is unknown if the closed loop system is guaranteed to be stable. This is certainly a problem if either one of the controllers is unstable.
A Youla based solution
To resolve the latter issues, one can proceed according to the approach suggested in [11], [12]. This proceeds as follows.
Let ![]() be a proper LTI system that admits the realization
be a proper LTI system that admits the realization
![Rendered by QuickLaTeX.com \[G=\left(\begin{array}{cc}G_{11}&G_{12}\\G_{21}& G_{22}\end{array}\right)=\left[\begin{array}{c|cc}A&B_1&B_2\\ \hline C_1&D_{11} &D_{12}\\ C_1&D_{21} &D_{22} \end{array}\right],\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-07159522c50d5c5b93510c3ce723a0d3_l3.png?media=1702023987)
![]()
This can be done using the function fCoprime (details). Given ![]() and the eight transfer matrices that satisfy the Bezout identity, one then can arrive at an entire family of controllers that internally stabilize
and the eight transfer matrices that satisfy the Bezout identity, one then can arrive at an entire family of controllers that internally stabilize ![]() .
.
This parameterization is given by
![]()
Note that ![]() can also be written as a lower LFT of some fixed transfer matrix
can also be written as a lower LFT of some fixed transfer matrix ![]() and the Youla parameter
and the Youla parameter ![]() :
:
![]()
![]()
![]()
![]()
When ![]() is fixed for all
is fixed for all ![]() , the Youla parameter
, the Youla parameter ![]() is stable, which also implies that the control interconnection of the latter figure is stable. Hence, for any trajectory
is stable, which also implies that the control interconnection of the latter figure is stable. Hence, for any trajectory ![]() during the switching phase, the resulting controller can be regarded as a linear time varying system. In [11] it is shown that also for this case, the closed-loop system will remain stable.
during the switching phase, the resulting controller can be regarded as a linear time varying system. In [11] it is shown that also for this case, the closed-loop system will remain stable.
Note in case ![]() is already stable, i.e.,
is already stable, i.e., ![]() , then the matrices in the Bezout identity may be taken as:
, then the matrices in the Bezout identity may be taken as:
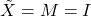
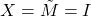
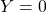 ,
, 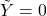
In this case, we obtain ![]() with the Youla parameter
with the Youla parameter ![]() .
.
Implementation
The function ![]() implements the described procedure. Here:
implements the described procedure. Here:
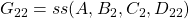 is the part of the plant seen by the controller. This realization must be stabilizable and detectable.
is the part of the plant seen by the controller. This realization must be stabilizable and detectable.- The controllers
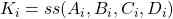 ,
, 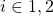 , which both stabilize
, which both stabilize 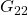 .
.
As output this yields:
- The transfer matrix
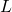 with realization
with realization 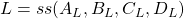
- The structure
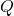 with the Youla parameters
with the Youla parameters  .
.
These can be interconnected as ![]() in accordance with the figure above, or, in case of more than two controllers as
in accordance with the figure above, or, in case of more than two controllers as ![]() with
with ![]() .
.
Note: The algorithms works for continuous- as well as discrete-time systems.
Demonstrating example
A demonstration of this procedure is found here.
