The file Demo_009.m is found in IQClab’s folder demos; it performs a robust controller synthesis with the function fRobsyn. This demo consists of the 2DoF control design for a plant with parametric uncertainty. The plant, ![]() , is a simple oscillator model, which is interconnected as shown in the following figure.
, is a simple oscillator model, which is interconnected as shown in the following figure.

Here ![]() is defined by the transfer function
is defined by the transfer function
![]()
where ![]() is the time-constant and
is the time-constant and ![]() the damping factor. Here
the damping factor. Here ![]() is a fixed constant, while
is a fixed constant, while ![]() is assumed to be an uncertain parameter
is assumed to be an uncertain parameter ![]() with
with ![]() and
and ![]() . The bode diagram for various samples of
. The bode diagram for various samples of ![]() is shown in the following figure.
is shown in the following figure.
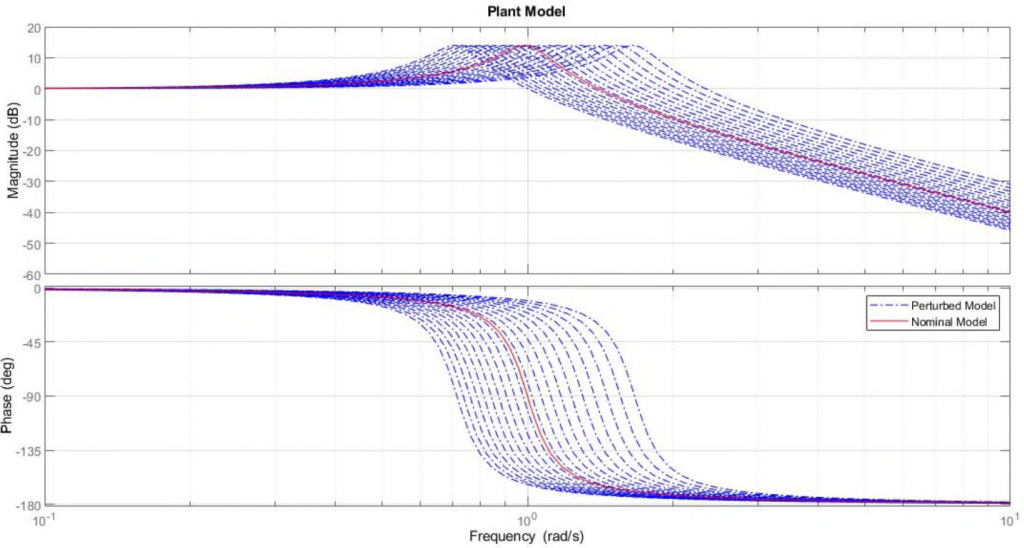
The goal is to design a 2DoF controller, ![]() , which stabilizes the plant
, which stabilizes the plant ![]() for all
for all ![]() , and which renders the induced
, and which renders the induced ![]() -gain on the weighted performance channels
-gain on the weighted performance channels ![]() satisfied. Here the aim is to enforce good tracking at low frequencies, while penalizing control at high frequencies.
satisfied. Here the aim is to enforce good tracking at low frequencies, while penalizing control at high frequencies.
This is accomplished with the performance weights
![]()
The generalized plant can be constructed as usual (see code in Demo_009.m). Subsequently, you can perform a nominal and robust controller synthesis by means of hinfsyn/fHinfsyn and fRobsyn respectively. The corresponding code is given next.
- Length of the basis function: 3
- Solution check: ‘on’
- Enforce strictness of the LMIs:

% Define the uncertain plant model
k0 = 1;
d = 0.1;
delta = ureal('delta',0,'Range',[-1,1],'AutoSimplify','full');
k = k0*(1+0.4*delta);
G = tf(1,[k^2,2*d*k,1]);
[H,De] = lftdata(G);
H = ssbal(H);
% Define the open-loop generalized plant
systemnames = 'H';
inputvar = '[p{2};r;u]';
outputvar = '[H(1:2);r-H(3);u;r;H(3)]';
input_to_H = '[p(1:2);u]';
cleanupsysic = 'yes';
olic = sysic;
% Define weights
Wperf = 1/makeweight(1e-3,1,2);
Wcmd = makeweight(1e-1,10,10);
Wout = blkdiag(1,1,Wperf,Wcmd,1,1);
wolic = Wout*olic;
% Perform a nominal controller synthesis
[Knom,~,ga_nom] = fHinfsyn(wolic(3:end,3:end),2,1,'method','lmi');
% Define iqc uncertainty block
de = iqcdelta('de','InputChannel',1:2, 'OutputChannel',1:2,'Bounds',[-1,1]);
de = iqcassign(de,'ultis','Length',2);
% perform a robust controller synthesis
options.maxiter = 5;
options.subopt = 1.01;
options.constants = 1e-6*ones(1,3);
options.Pi11const = 1e-5;
options.FeasbRad = 1e5;
[K,ga] = fRobsyn(wolic,de,[2,2,2],[2,1,1],options);
For the nominal controller, ![]() , we obtain an
, we obtain an ![]() -norm of approximately 1. However, when performing an IQC-analysis, the worst-case performance is in fact about 10 times larger. The robust controller,
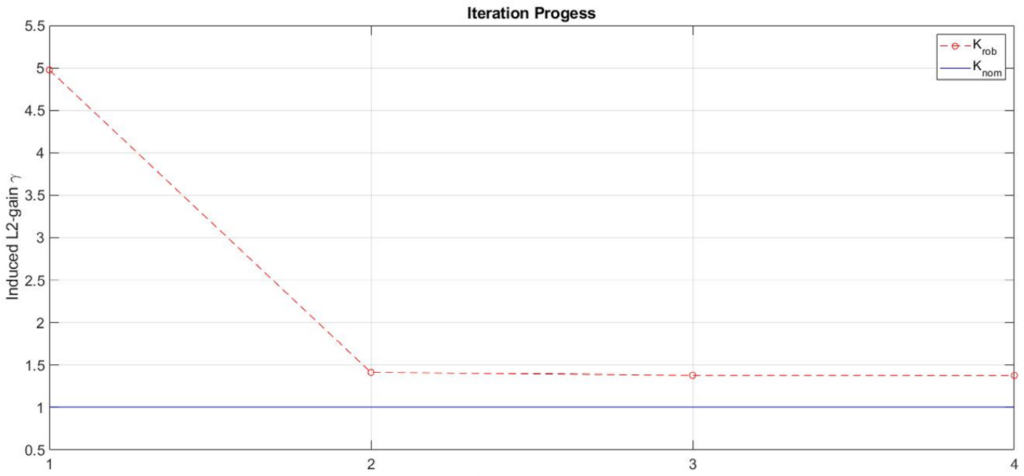
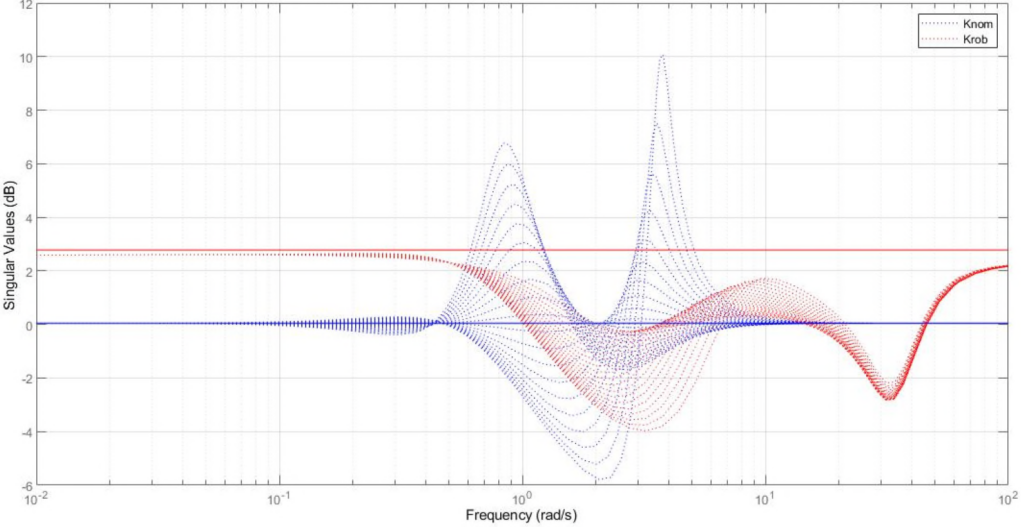
-norm of approximately 1. However, when performing an IQC-analysis, the worst-case performance is in fact about 10 times larger. The robust controller, ![]() , on the other hand, guarantees that the worst-case performance is not larger than 1.37, which is much closer to nominal performance level. This is illustrated in the following two figures. As can be seen in the first figure, the function fRobsyn quickly converges after four iterations to a worst-case performance of 1.37. This is confirmed by the second figure, where the sigma plots of the weighted closed loop system are shown for various samples of
, on the other hand, guarantees that the worst-case performance is not larger than 1.37, which is much closer to nominal performance level. This is illustrated in the following two figures. As can be seen in the first figure, the function fRobsyn quickly converges after four iterations to a worst-case performance of 1.37. This is confirmed by the second figure, where the sigma plots of the weighted closed loop system are shown for various samples of ![]() for both the nominal controller,
for both the nominal controller, ![]() as well as the robust controller
as well as the robust controller ![]() .
.
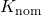 and
and  .
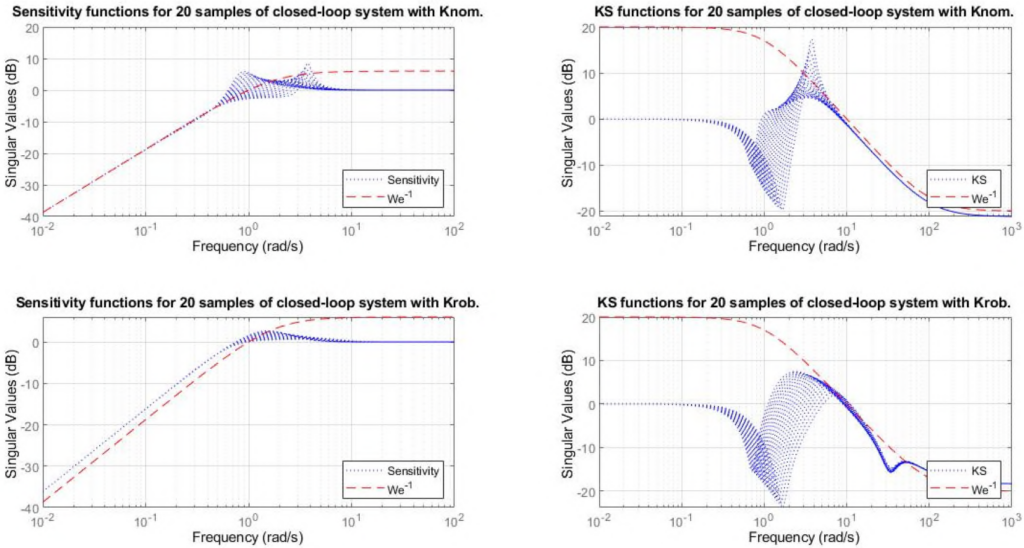
.To continue, the following figure shows the singular value plots of the sensitivity and control sensitivity function ![]() and
and ![]() respectively, for various samples of
respectively, for various samples of ![]() versus the inverse weighting functions that were used in the controller synthesis. Again, we conclude that the robust controller,
versus the inverse weighting functions that were used in the controller synthesis. Again, we conclude that the robust controller, ![]() is better capable of guaranteeing performance in the presence of the uncertainty. This is confirmed by the time domain simulation shown in the last figure.
is better capable of guaranteeing performance in the presence of the uncertainty. This is confirmed by the time domain simulation shown in the last figure.
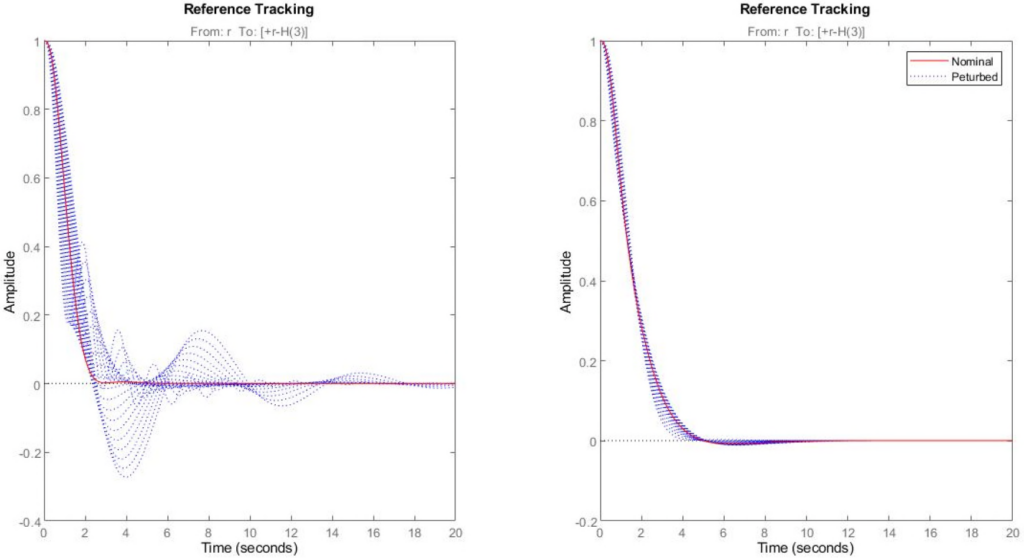
![Rendered by QuickLaTeX.com \delta\in[-1,1]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-cdc512599dd4884aa5ed731b8f497e43_l3.png?media=1702023987) – left: nominal controller,
– left: nominal controller, 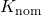 – right: robust controller,
– right: robust controller,  .
.