The file Demo_008.m is found in IQClab’s folder demos; it performs an LPV controller synthesis with the function fLPVsyn. The example is taken from [16]. This paper describes the application of the LPV control design algorithm to a parametrically varying flight control problem. The LPV model together with the performance objectives are found in this reference.
The equations of motion are given by:
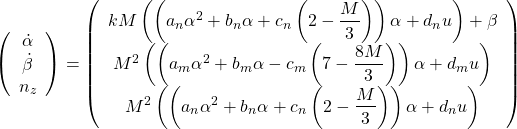
Here:
![Rendered by QuickLaTeX.com \alpha\in[0,\pi/9]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-065bf23d458d75947612ea5ed2b87bb6_l3.png?media=1702023987) is the angle-of-attack (rad)
is the angle-of-attack (rad)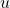 is the tail fin deflection (rad)
is the tail fin deflection (rad)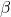 is the pitch rate (rad/s)
is the pitch rate (rad/s)![Rendered by QuickLaTeX.com M\in[2,4]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-4b36ee304a6aa16fe9226b4b11b66eb7_l3.png?media=1702023987) is the Mach number
is the Mach number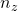 is the normal acceleration per
is the normal acceleration per 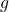
The remaining constants are given by
The synthesis objective is to track the commanded acceleration manoeuvres ![]() , while satisfying some performance specifications. The control input is the tail fin deflection
, while satisfying some performance specifications. The control input is the tail fin deflection ![]() , and the measurements are the error in nominal acceleration and the pitch rate:
, and the measurements are the error in nominal acceleration and the pitch rate:
![]()
We choose the reference ![]() for the normal acceleration as the exogenous performance outputs as:
for the normal acceleration as the exogenous performance outputs as:
![]()
with the performance weight
![Rendered by QuickLaTeX.com \[W_p=\left(\begin{array}{cc}\dfrac{0.5(s+7)}{(s+3.5\cdot 10^{-6})}&0\\0& \dfrac{4.444\cdot 10^{7}(s+9)}{(s+2\cdot 10^{6})} \end{array}\right)\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-53c950b869cde90b24f44ead3fac8c3b_l3.png?media=1702023987)
in order to enforce disturbance rejection at low frequencies and to penalized control actuation at high frequencies.
To derive the LPV model, we conveniently choose the Mach number, ![]() , and the angle of attack,
, and the angle of attack, ![]() , as scheduling variables. Then it is not difficult to formulate an LFT structure of the equations of motion with normalized scheduling block
, as scheduling variables. Then it is not difficult to formulate an LFT structure of the equations of motion with normalized scheduling block
![]()
where ![]() and
and ![]() .
.
The synthesis was run with the following code:
- Length of the basis function: 3
- Solution check: ‘on’
- Enforce strictness of the LMIs:

% Load missile open-loop plant
load missile
% Define uncertainties
del_a = ureal('del_a',0,'Range',[-1,1]);
del_M = ureal('del_M',0,'Range',[-1,1]);
Del_a = pi/18*(1 + del_a);
Del_M = 3 + del_M;
Del_T = blkdiag(Del_a*eye(2),Del_M*eye(5));
% Extract open-loop interconnection for normalized uncertainties
P = lft(Del_T,ssbal(G));
[olic,De] = lftdata(P);
% Append weighting functions
wp = ss(tf([0.5,3.5],[1,3.5e-6]));
wu = ss(20*tf([1/0.9,1],[1e-6,1]));
Wo = ssbal(blkdiag(eye(7),wp,wu,eye(2)));
wolic = Wo*ssbal(olic);
% Define scheduling block
H{1} = blkdiag(eye(5),zeros(2));
H{2} = blkdiag(zeros(5),eye(2));
La = polydec(pvec('box',[-1,1;-1,1]))';
iqcdeltaOpt.InputChannel = 1:7;
iqcdeltaOpt.OutputChannel = 1:7;
iqcdeltaOpt.Polytope = La;
iqcdeltaOpt.UncertaintyMap = H;
iqcdeltaOpt.TimeInvTimeVar = 'TV';
iqcdeltaOpt.Structure = 'FB';
Delta = iqcdelta('Delta',iqcdeltaOpt);
% Define synthesis options
options.RelaxType = 'CH';
options.FeasbRad = 1e8;
options.constants = [1e-8,1e-7,1e-7,1e-9,1e-8,1e-8];
options.subopt = 1.1;
options.bounds = [1e5,1,1e5,1];
% Perform synthesis
[K,ga] = fLPVsyn(wolic,Delta,[7,2,2],[7,1,1],options);
Here
- The chosen relaxation type is convex hull (CH),
- The feasibility radius is confined to
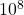 ,
, - The LMI constraints are perturbed by the constants
![Rendered by QuickLaTeX.com 10^{-8}[1,10,10,1,1,1]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-441637813d3b9509068ef9e075cb871b_l3.png?media=1702023987) ,
, - A sub-optimal solution is computed, while
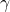 is relaxed with 10% and while the norms are minimized with options.bounds=
is relaxed with 10% and while the norms are minimized with options.bounds=![Rendered by QuickLaTeX.com [10^5,1,10^5,1]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-85fd6e9c4e3f57165201297d74bd130b_l3.png?media=1702023987) .
.
This yields the LTI part of the controller, ![]() , together with the obtained sub-optimal induced
, together with the obtained sub-optimal induced ![]() -gain,
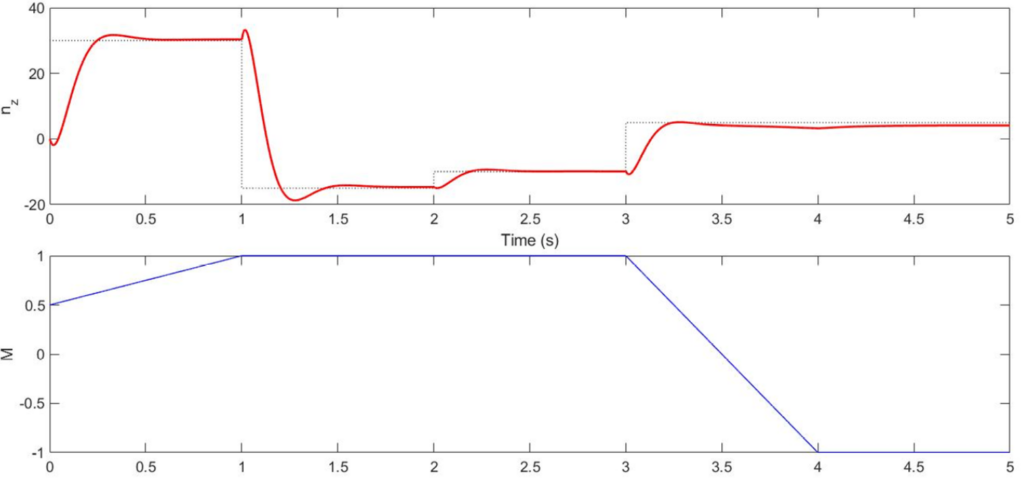
-gain, ![]() . The time-domain simulation results are shown in the following figure.
. The time-domain simulation results are shown in the following figure.