IQClab also includes tools for performing parametric sensitivity analyses for uncertain LTI systems that are affected by parametric uncertainties. The aim here is to identify driving uncertainties, i.e., identify which uncertainties affect the system’s performance the most and quantify by how much.
Such analyses can be performed with the function
out = sensanalysis(P,meth,N,plotonoff).
Here:
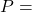 lft
lft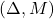 is an LFT, which is composed of the stable LTI plant
is an LFT, which is composed of the stable LTI plant 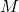 (continuous or discrete time) and the uncertainty block.
(continuous or discrete time) and the uncertainty block.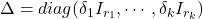 , where the uncertain parameters are objects form the class ureal.
, where the uncertain parameters are objects form the class ureal.- meth is for specifying 1 of the 4 available methods (i.e., ‘spea’, ‘src’, ‘morris’, and ‘var’) for performing the sensitivity analysis. These are further discussed below.
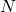 specifies the number of samples considered in the analysis.
specifies the number of samples considered in the analysis.- plotonoff=’on’/’off’ is an optional input that allows turning ‘off’ the generation of plots within the function (default is ‘on’ ). By default, the function generates a plot visualizing the computed outcome of the analysis.
Note: In case (some of) the uncertainties are not normalized, then they are normalized internally as ![]() before performing the analysis.
before performing the analysis.
All methods compute the effect of each of the uncertainties in the output for the function ![]() , which is the
, which is the ![]() -norm of
-norm of ![]() for some
for some ![]() , with
, with ![]() being defined by
being defined by ![]() ,
, ![]() .
.
Spearman rank correlation
The option ‘spea’ computes the Spearman rank correlation ![]() (see e.g., [25]), which is defined as
(see e.g., [25]), which is defined as
![Rendered by QuickLaTeX.com \[\rho_{\delta_i,y}=\frac{\Sigma_{j=1}^N(\delta_i^j-\bar{\delta}_i)(y^j-\bar{y})}{\sqrt{\Sigma_{j=1}^N(\delta_i^j-\bar{\delta}_i)^2\cdot \Sigma_{j=1}^N(y^j-\bar{y})^2}}\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-7a4c7f34d500cffb903eebeaee0b752e_l3.png?media=1702023987)
The higher the value of ![]() , the more sensitive the system is to the uncertainty
, the more sensitive the system is to the uncertainty ![]() .
.
This is a so-called “local” one-at-the-time (OAT) analysis approach, which requires the least amount of computational effort (compared to the other approaches). The other methods can be interpreted as “global” techniques, which also (intend to) address the cross-correlation between the parameters.
As output, one obtains the structure out with the fields:
- out.rho: This is the vector with the computed sensitivity indices
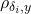 ,
,  , in descending order (hence the first parameter is identified as the most sensitive one).
, in descending order (hence the first parameter is identified as the most sensitive one). - out.unc: This is the vector with the names of the uncertainties ordered corresponding to the computed sensitivity indices provided in out.rho.
Standard regression coefficients
The option ‘src’ computes the standard regression coefficients (see e.g., [25])
![]()
![]()
As output, one obtains the structure out with the fields:
- out.src: This is the vector with the computed sensitivity indices
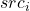 ,
, 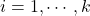 , in descending order (hence the first parameter is identified as the most sensitive one).
, in descending order (hence the first parameter is identified as the most sensitive one). - out.unc: This is the vector with the names of the uncertainties ordered corresponding to the computed sensitivity indices provided in out.src.
Morris method
With the option ‘morris’ the function computes so-called elementary effects [26], [25]. The elementary effect of the ![]() input is defined as
input is defined as
![]()
![]()
![Rendered by QuickLaTeX.com \[\sigma_i=\sqrt{\dfrac{\Sigma_{j=1}^N(d_i(j)-\mu_i)^2}{N}}.\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-b0f9ca392c16190f00bde1eec4dc5cf7_l3.png?media=1702023987)
The higher the value of ![]() , the more sensitive the output
, the more sensitive the output ![]() is to variations in the input
is to variations in the input ![]() . On the other hand, the higher the value of
. On the other hand, the higher the value of ![]() , the more interaction
, the more interaction ![]() has with the other inputs.
has with the other inputs.
For economical sampling strategies, Morris [26] proposed the following approach in which ![]() is even and
is even and ![]() as suggested above. The method consists of selecting the random orientation matrix
as suggested above. The method consists of selecting the random orientation matrix
![]()
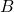 is a lower triangular matrix of dimension
is a lower triangular matrix of dimension 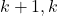 padded with ones,
padded with ones,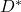 is a
is a 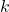 -dimensional diagonal matrix in which each diagonal entry is either
-dimensional diagonal matrix in which each diagonal entry is either 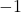 or
or 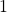 with equal probability,
with equal probability,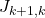 is a
is a 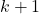 by
by 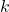 all ones matrix and
all ones matrix and 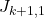 the all ones vector of dimension
the all ones vector of dimension 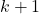 by
by 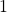 ,
,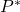 is a random permutation matrix in which each column contains one element being equal to
is a random permutation matrix in which each column contains one element being equal to 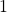 , while all other entries are
, while all other entries are 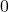 ,
,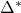 is a randomly chosen ‘base value’ of
is a randomly chosen ‘base value’ of 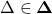 for which each element is randomly assigned a value from the grid
for which each element is randomly assigned a value from the grid 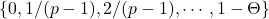 .
.
As output, one obtains the structure out with the fields:
- out.mu: This is the vector with the computed sensitivity indices
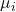 ,
, 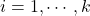 , in descending order (hence the first parameter is identified as the most sensitive one).
, in descending order (hence the first parameter is identified as the most sensitive one). - out.std: This is the vector with the computed sensitivity indices
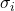 ,
, 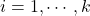 , ordered corresponding to the computed sensitivity indices provided in out.mu.
, ordered corresponding to the computed sensitivity indices provided in out.mu. - out.unc: This is the vector with the names of the uncertainties ordered corresponding to the computed sensitivity indices provided in out.mu.
Variance-based approach
With the option ‘var’ the function computes the effect of each uncertainty with respect to its induced variance in the output [27]. Given the model ![]() the variance-based metrics, the so-called first-order and total effect, are given by
the variance-based metrics, the so-called first-order and total effect, are given by
![]()
![]()
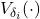 and
and 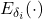 denote the variance and mean of the argument taken over
denote the variance and mean of the argument taken over  ,
,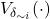 and
and 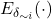 denote the variance and mean of the argument taken over
denote the variance and mean of the argument taken over  except for
except for  .
.
The indices ![]() and
and ![]() can be interpreted as:
can be interpreted as:
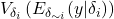 is the expected reduction in variance that would be obtained if
is the expected reduction in variance that would be obtained if  could be fixed,
could be fixed,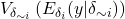 is the expected variance that would be left if all factors but
is the expected variance that would be left if all factors but  could be fixed.
could be fixed.
There are several ways to compute ![]() and
and ![]() . In the present function, they are computed as:
. In the present function, they are computed as:
![Rendered by QuickLaTeX.com \[S_i=\frac{V(y)-\frac{1}{2N}\Sigma_{j=1}^N\left(f(\mathbf{B})_j-f(\mathbf{A}_{\mathbf{B}}^{(i)})_j\right)^2}{V(y)}\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-95959e9ff8f07771dcbf9736c144c8cd_l3.png?media=1702023987)
and
![Rendered by QuickLaTeX.com \[S_{Ti}=\frac{\frac{1}{2N}\Sigma_{j=1}^N\left(f(\mathbf{A})_j-f(\mathbf{A}_{\mathbf{B}}^{(i)})_j\right)^2}{V(y)}.\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-bc09657a9bfb7d87d0c1871736c6c8db_l3.png?media=1702023987)
Here ![]() ,
, ![]() are
are ![]() by
by ![]() matrices with samples taken from the set
matrices with samples taken from the set ![]() ; in this function according to a uniform distribution (i.e., other distributions, such as pseudo random distribution, are also possible, but would require the statistics and machine learning toolbox). The matrix
; in this function according to a uniform distribution (i.e., other distributions, such as pseudo random distribution, are also possible, but would require the statistics and machine learning toolbox). The matrix ![]() is a composition of the matrix
is a composition of the matrix ![]() , while its
, while its ![]() column is replaced with the corresponding column of
column is replaced with the corresponding column of ![]() .
.
As output, one obtains the structure out with the fields:
- out.STi: This is the vector with the computed sensitivity indices
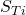 ,
, 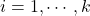 , in descending order (hence the first parameter is identified as the most sensitive one).
, in descending order (hence the first parameter is identified as the most sensitive one). - out.Si: This is the vector with the computed sensitivity indices
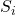 ,
, 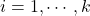 , ordered corresponding to the computed sensitivity indices provided in out.STi.
, ordered corresponding to the computed sensitivity indices provided in out.STi. - out.unc: This is the vector with the names of the uncertainties ordered corresponding to the computed sensitivity indices provided in out.STi.
Demonstrating example
A demonstration of this function is found here.
