Once all uncertainty blocks have been defined and all IQC-multipliers have been assigned, one can proceed by performing an IQC analysis by means of the function iqcanalysis.
This function supports the computation of the following performance metrics:
- Induced
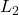 -gain performance
-gain performance 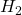 performance (deterministic signal-based interpretation)
performance (deterministic signal-based interpretation)- Generalized
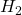 performance (energy to peak)
performance (energy to peak) - Passivity performance
If no performance blocks are specified, the algorithm performs a robust stability analysis.
The function can be called as follows:
![]()
 is the uncertain stable continuous- or discrete time LTI plant
is the uncertain stable continuous- or discrete time LTI plant is the main uncertainty/performance block, which is assumed to be bounded on
is the main uncertainty/performance block, which is assumed to be bounded on 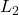 and whose entries are objects from the class iqcdelta, which have been associated with an IQC multiplier using iqcassign. The uncertainty/performance block
and whose entries are objects from the class iqcdelta, which have been associated with an IQC multiplier using iqcassign. The uncertainty/performance block 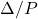 should be provided as a cell:
should be provided as a cell:
Here the order of the blocks is not relevant.![Rendered by QuickLaTeX.com \[\Delta=\{\Delta_1,\ldots,\Delta_N,P_1,\ldots,P_M\}.\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-471d0b25a3afb9f2639d24bd89d650f0_l3.png?media=1702023987)
- The option varargin allows specifying additional properties in the IQC-analysis. This proceeds in the following fashions as discussed in the following table.
| Option | Description |
| 1 | For |
| 2 | The properties can also be set by defining a structure and subsequently specifying |
| 3 | Finally, the properties can be set and retrieved respectively by and |
The following table provides an overview of properties that can be set in the IQC-analysis.
| Property | Description |
| Parser | It is possible to select either one of the following parsers: 1. ‘LMIlab’ (default) 2. ‘Yalmip’ Note: It is emphasized that the use of Yalmip in combination with whichever solver sometimes seems less reliable if compared to the use of LMIlab. To this end, it is always recommended to perform a post-solution check to confirm that a solution is indeed feasible (see Property SolChk for more details). |
| Solver | If selecting LMIlab, the Matlab solvers mincx, and feasb are used to solve the minimization and feasibility problem respectively. On the other hand, if using Yalmip, you can consider various solvers, such as e.g., mosek, sdpt3, sedumi, etc. The reader is referred to https://yalmip.github.io/allsolvers/ for an overview of solvers that are supported. |
| gmax | ‘gmax’ specifies the maximum worst-case performance value (default = 1e4). |
| FeasbRad | ‘FeasbRad’ specifies the feasibility radius (default = 1e9). |
| RelAcc | ‘RelAcc’ is an LMIlab option that specifies the relative accuracy on the computed optimal value (default = 1e-6). |
| MaxNumIter | ‘MaxNumIter’ is an LMIlab option that specifies the maximum number of iterations that can be performed by the optimization procedure (default = 800). |
| Terminate | ‘Terminate’ is an LMIlab option that helps speeding up the termination. If set to an integer value |
| Display | ‘Display’ allows to turn on/off the trace of execution of the optimization procedure (default = ‘off’). |
| Init | The option ‘Init’ can be used to specify an initial condition for the LMI optimization problem (default = []). |
| eps | ‘eps’ allows to enforce strict LMI by a small nonnegative constant (default = 1e-9) |
| SolChk | ‘SolChk’ allows to verify whether an obtained LMI solution is indeed feasible (default = ‘off’) |
| Pi11pos | To improve the conditioning of the IQC-multiplier sub-block To do so, one can specify ‘ Pi11pos’ (default = 0). Note: |

![Rendered by QuickLaTeX.com \[\begin{array}{c} options.prop1=value1\\\vdots\\options.propN=valueN\end{array}\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-7bcf7fef0e4df94946fe846d0911664c_l3.png?media=1702023987)