ups: Passive uncertainties

The class ups is defined by uncertainties/nonlinearities of the form $\Delta_\mathrm{ups}:L_2^{n_{in}}\rightarrow L_2^{n_{out}}$ with

Dimension $n_{out}\times n_{in}$
$\langle q,\Delta(q)\rangle\geq0$

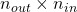
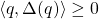
The ups class can be defined by

$\Delta_\mathrm{ups}=ups('name')$
$\Delta_\mathrm{ups}=ups('name',varargin)$

Just specifying $\Delta_\mathrm{ups}=ups('name')$ defines a scalar passive uncertainty/ nonlinearity.

Specifying and/or changing properties proceeds as summarized in the following two tables for properties related to the uncertainty and to IQC-multiplier respectively.

\[\begin{array}{c} InputChannel=\left[\! \! \! \begin{array}{ccc}C_{x}^{in}&\cdots&C_{y}^{in}\end{array} \! \! \! \right]\\OutputChannel=\left[ \! \! \! \begin{array}{ccc}C_{v}^{in}&\cdots&C_{w}^{in}\end{array} \! \! \! \right] \end{array}\] — Uncertainty characteristics

Note: See Section 5.6 of [1] for the details on the mathematical derivation of the IQC-multiplier.

Property	Description
Dimension	Specify the dimension of the uncertainty/ nonlinearity (default = 1).
InputChannel/ OutputChannel	Specify which input and output channels of the uncertain plant are affected by $\Delta_\mathrm{ups}$ . The channels should be specified as: $\begin{array}{c} InputChannel=\left[\! \! \! \begin{array}{ccc}C_{x}^{in}&\cdots&C_{y}^{in}\end{array} \! \! \! \right]\\OutputChannel=\left[ \! \! \! \begin{array}{ccc}C_{v}^{in}&\cdots&C_{w}^{in}\end{array} \! \! \! \right] \end{array}$ Here the order of the channels is not relevant, while $C_{m}^{in}$ , $C_{n}^{out}$ respectively denote the $m^{th}$ and $n^{th}$ in- and output channel of the uncertain plant $M$ .

Property	Description
BasisFunctionType	Specify the type of basis function to be used in the multiplier (default = 1). See link for further details.
Length	Specify the length of the basis function (default = 1). See link for further details. Note: It is not always allowed to set $Length>1$ .
PoleLocation	Specify the pole location of the basis function (default = -1). See link for further details.
SampleTime	Specify the sample time (default = 0).
PrimalDual	Specify whether the multiplier should be a primal/dual parametrization (default = ‘Primal’). – Primal multipliers: ‘Primal’ – Dual multipliers: ‘Dual’ Note: For a standard IQC-analysis, all multipliers must be primal ones.