Create LMIs – IQClab

The function iqclmi facilitates the definition of new LMI constraints. In the present version of the toolbox, this is limited to generating LMIs of the form

$JC^TB^TPBC\succcurlyeq JC^TAC+\epsilon I.$

Here:

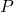$P$ is a symmetric structured matrix variable defined with the class iqcvar
$J$ is the inertia of the LMI (i.e., $J=1$ and $J=-1$ mean positive- and negative definite respectively)
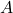$A$ is a constant symmetric matrix
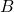$B$ is a constant matrix
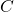$C$ is a constant matrix (e.g., an annihilator)
$\epsilon$ is a small constant enforcing the LMI to be strict (this constant can be modified by changing the property eps in the iqcprob class

Note: It is emphasized that all LMIs can be written in this form. Clearly, this still requires some additional parsing. In future releases the aim is to further mature this.

Specifying LMIs proceeds as follows.

Previous page, Next page

Input	Output
$iqcprob=iqclmi(iqcprob,P,J)$	This generates the LMI $JP\succcurlyeq\epsilon I$
$iqcprob=iqclmi(iqcprob,P,J,A)$	This generates the LMI $JP\succcurlyeq JA+\epsilon I$
$iqcprob=iqclmi(iqcprob,P,J,A,B)$	This generates the LMI $JB^TPB\succcurlyeq JA+\epsilon I$
$iqcprob=iqclmi(iqcprob,P,J,A,B,C)$	This generates the LMI $JC^TB^TPBC\succcurlyeq JC^TAC+\epsilon I$