The file Demo_011.m is found in IQClab’s folder demos. In this demo we demonstrate the Youla-based switching approach presented here.
Let us consider the first order system
![]()
where ![]() . In addition,
. In addition, ![]() is assumed to be affected by the multiplicative dynamic uncertainty
is assumed to be affected by the multiplicative dynamic uncertainty
![]()
where ![]() and
and ![]() .
.
We consider a standard tracking configuration yielding the open-loop generalized plant interconnection ![]() , given by:
, given by:
![Rendered by QuickLaTeX.com \[\left(\begin{array}{c}z_1\\z_2\\z_3\\y\end{array}\right)=\left(\begin{array}{ccc}I&0&-G\\0&0&I\\0&0&G\\I&-I&-G\end{array}\right) \left(\begin{array}{c}r\\n\\u\end{array}\right)\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-f4615e1cb2f48b01e9154b654228a109_l3.png?media=1702023987)
Here ![]() ,
, ![]() , and
, and ![]() are the reference, noise, and control input, respectively, while
are the reference, noise, and control input, respectively, while ![]() ,
, ![]() ,
, ![]() , and
, and ![]() denote the tracking error, control input, plant output, and measurement input.
denote the tracking error, control input, plant output, and measurement input.
We consider two PI controllers
![]()
and implement two mode switching schemes between ![]() and
and ![]() :
:
- Classical switch:

- Youla-based switch:
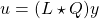 , where
, where 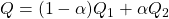 , where
, where 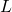 ,
, 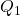 , and
, and 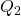 are constructed from the plant and the controllers
are constructed from the plant and the controllers 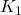 and
and 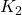 by the function fYoulaSwitch (see details here).
by the function fYoulaSwitch (see details here).
In both cases, ![]() is the switching parameter. In the simulations, this parameter is varied in two fashions:
is the switching parameter. In the simulations, this parameter is varied in two fashions:
- Instantaneous switch:
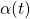 is switched from 0 to 1 instantaneously
is switched from 0 to 1 instantaneously - Smooth switch:
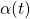 is switched from 0 to 1 by slowly increasing its value
is switched from 0 to 1 by slowly increasing its value
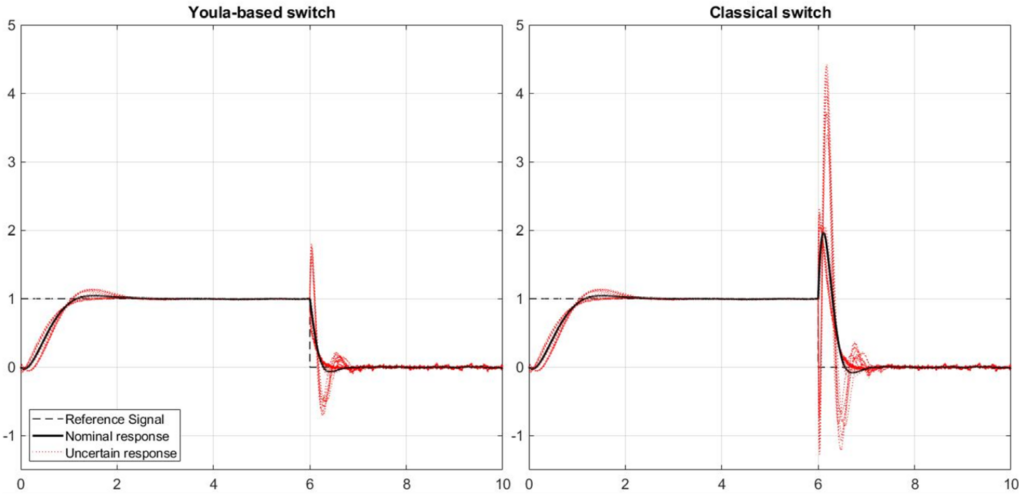
The following two figures show the nominal and uncertain simulation step responses for the instantaneous and smooth switching scenario for both the classical as well as the Youla-based switching scheme respectively.
Regarding the instantaneous switching in the first figure, we conclude that:
- Nominal performance is significantly better for the Youla based implementation, where stability is guaranteed for the nominal case (i.e for this demonstration, we did not bother to address robustness issues with respect to the plant uncertainties).
- Even if we also see a degradation of performance for the Youla based approach in case the plant uncertainties are included, we clearly see a robustification if compared to the classical implementation.
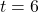 seconds)
seconds)Regarding the smooth switching in the next figure, we conclude that:
- In both cases performance can be significantly improved if compared to instantaneous switching.
- Moreover, also for this scenario, the Youla based implementation outperforms the classical one in both the nominal as well as the uncertain cases.
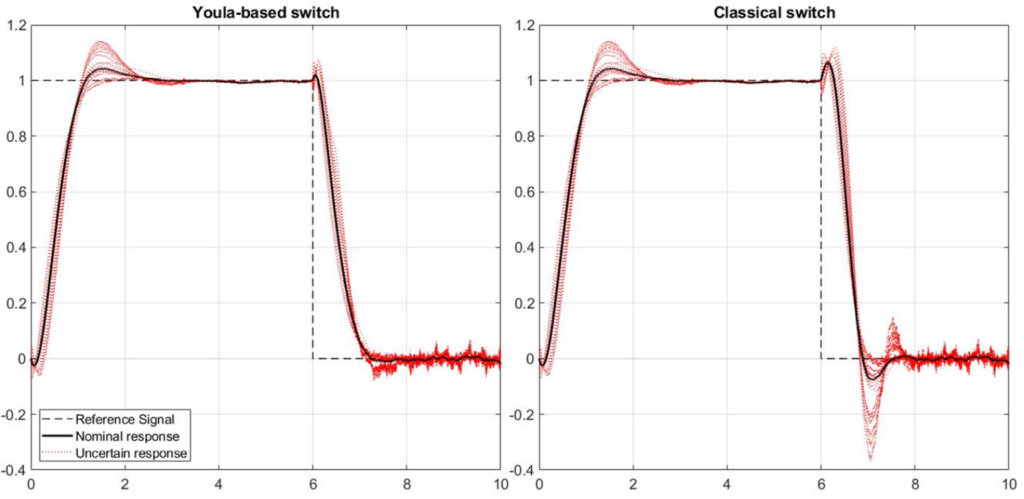
![Rendered by QuickLaTeX.com t\in[6,7]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-accd9bdf7302602003f5e3ab549e7991_l3.png?media=1702023987) seconds)
seconds)Further remarks:
- The switching between the different controllers in the presented demo was performed while the controller was tracking a reference input (i.e. not while being in steady state). Clearly, switching while being in steady state will have much less of an impact. However, this might not always be possible.
- The Youla-based switching implementation has as drawback that the control order will increase. The reader is referred to [11] for further details.
- With the IQC-analysis tools, one can easily perform a robustness analysis by including
![Rendered by QuickLaTeX.com \alpha(t)\in[0,1]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-19df1fbf9d5ef053ef0ecb7f47349a3f_l3.png?media=1702023987) as an uncertain parameter.
as an uncertain parameter.
