The file Demo_014.m is found in IQClab’s folder demos; it performs a robust estimator synthesis with the function fRobest for a mass-spring-damper problem derived from the example presented in [24]. The setup is shown in the following figure.
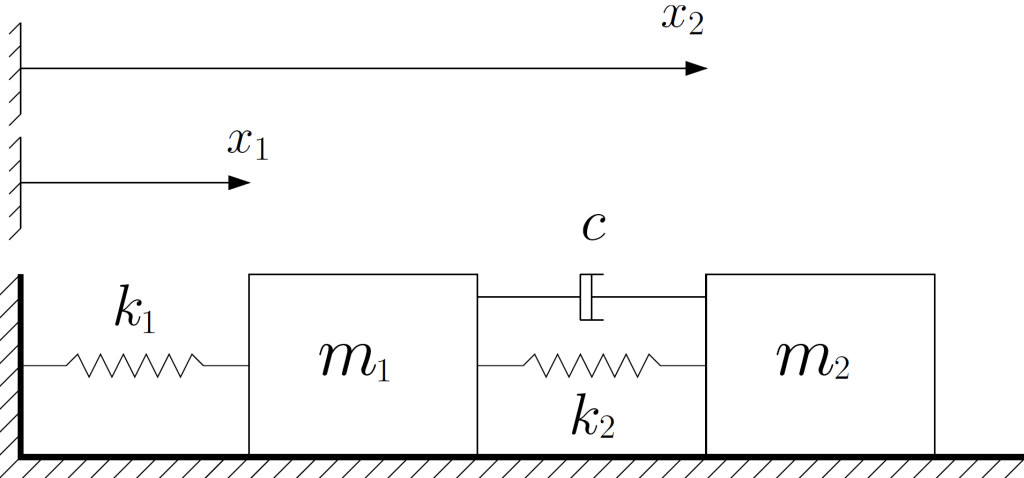
The numerical values are ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() with
with ![]() . The first mass is disturbed by an external force
. The first mass is disturbed by an external force ![]() . The objective is to estimate
. The objective is to estimate ![]() using a measument of
using a measument of ![]() corrupted by measurement noise
corrupted by measurement noise ![]() . The linear fractional representation can then be written as
. The linear fractional representation can then be written as
![Rendered by QuickLaTeX.com \left(\!\!\begin{array}{c}q_\mathrm{c}\\q_\mathrm{k}\\z\\y\end{array}\!\!\right)= \left[\!\!\begin{array}{cccc|cccc}0&0&1&0&0&0&0&0\\ 0&0&0&1&0&0&0&0\\ -2&1&-2&2&-1.75&-0.5&1&0\\ 2&-2&4&-4&3.5&1&0&0\\ \hline 0&0&1&-1&0&0&0&0\\ 1&-1&0&0&0&0&0&0\\ 0&1&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&1\end{array}\!\!\right] \left(\!\!\begin{array}{c}p_\mathrm{c}\\p_\mathrm{k}\\w_1\\w_2\end{array}\!\!\right)](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-44a45f6c429ed0109cb65839d3ca0bad_l3.png?media=1702023987)
with ![]() ,
, ![]() .
.
For comparison reasons, we design a nominal ![]() estimator,
estimator, ![]() , using the function ‘h2syn’, which is part of MATLAB’s robust control toolbox, as well as a robust
, using the function ‘h2syn’, which is part of MATLAB’s robust control toolbox, as well as a robust ![]() estimator,
estimator, ![]() , using the function ‘fRobest’, which is part of IQClab.
, using the function ‘fRobest’, which is part of IQClab.
The code for designing the nominal estimator is found in the file Demo_014.m. Designing the robust estimator proceeds as follows:
% Define plant (see script for system matrices)
H = ss(A,[Bp,Bw],[Cq;Cz;Cy],[Dqp,Dqw;Dzp,Dzw;Dyp,Dyw]);
% Define uncertainties
de1 = iqcdelta('de1','InputChannel',1,'OutputChannel',1, 'Bounds',[-1,1]);
de1 = iqcassign(de1,'ultis','Length',3);
de2 = iqcdelta('de2','InputChannel',2,'OutputChannel',2, 'Bounds',[-1,1]);
de2 = iqcassign(de2,'ultis','Length',3);
% set options
options.perf = 'H2';
options.StrProp = 'yes';
options.subopt = 1.03;
options.constants = 1e-8*ones(1,4);
options.Pi11pos = 1e-8;
options.FeasbRad = 1e9;
[Erob,gamrob] = fRobest(H,{de1,de2},[2,1,1],[2,2],options);
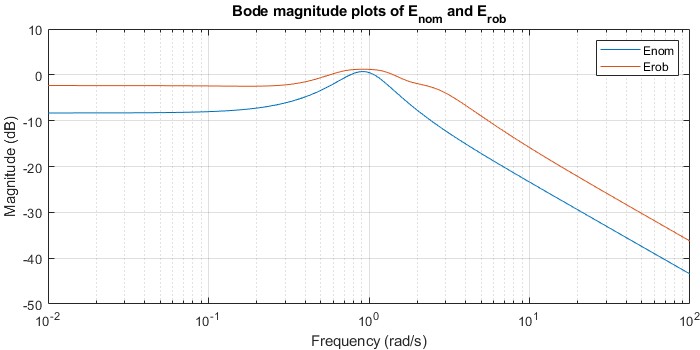
We obtain a nominal and robust estimator, ![]() and
and ![]() respectively, which guarantee a nominal and robust
respectively, which guarantee a nominal and robust ![]() performance level of
performance level of ![]() and
and ![]() respectively. The corresponding Bode-magnitude plots are depicted in the following figure.
respectively. The corresponding Bode-magnitude plots are depicted in the following figure.
Given ![]() and
and ![]() we can also perform a robustness analysis using the function ‘iqcanalysis’. This yields the following computed worst-case
we can also perform a robustness analysis using the function ‘iqcanalysis’. This yields the following computed worst-case ![]() perfomormance levels for increasing levels of
perfomormance levels for increasing levels of ![]() with
with ![]() ,
, ![]() .
.
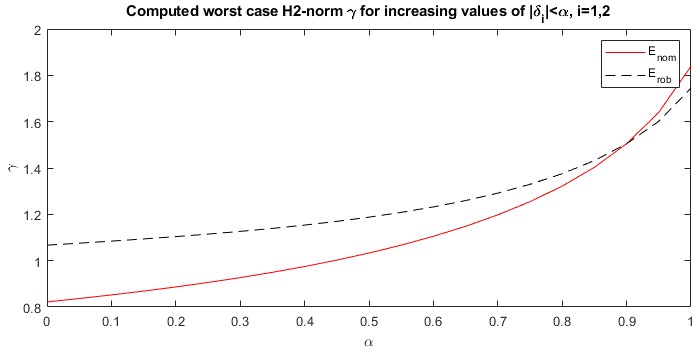
As can be seen, the nominal estimator, ![]() , shows better performance levels for smaller values of
, shows better performance levels for smaller values of ![]() , while for
, while for ![]() the robust estimator,
the robust estimator, ![]() , outperforms
, outperforms ![]() .
.
To continue, let us also show some time-domain simulations, where we perturb the system with a random force disturbance and for different values of ![]() . The results are shown in the following two figures for
. The results are shown in the following two figures for ![]() and
and ![]() respectively.
respectively.
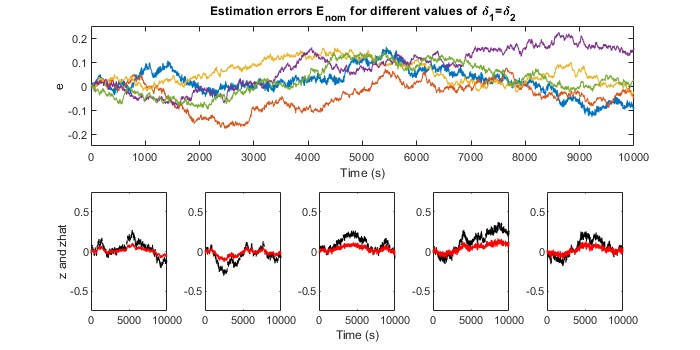
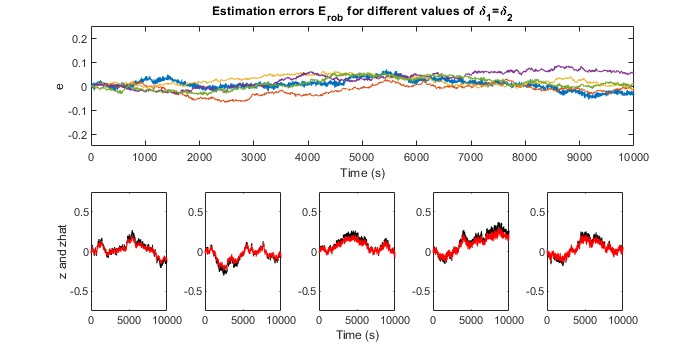
As can be seen, the robust estimator ![]() does a better job, if compared to
does a better job, if compared to ![]() . This is confirmed by the computed RMS values which are given in the following table.
. This is confirmed by the computed RMS values which are given in the following table.
| Mean | ||||||
| RMS value | 0.059 | 0.069 | 0.074 | 0.111 | 0.068 | 0.076 |
| RMS value | 0.022 | 0.026 | 0.028 | 0.043 | 0.026 | 0.029 |
