An IQC analysis starts with an LFT description of your uncertain plant. IQClab assumes that this description (i.e., the ![]() structure) is a given input, which is defined by (see [1] for the technical details):
structure) is a given input, which is defined by (see [1] for the technical details):
 is the performance channel
is the performance channel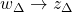 is the uncertainty channel
is the uncertainty channel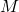 is a proper and stable (closed-loop) LTI system that admits a state space description, which can be defined either in continuous- or in discrete time
is a proper and stable (closed-loop) LTI system that admits a state space description, which can be defined either in continuous- or in discrete time is the uncertainty, which is assumed to have a diagonal block structure whose elements are bounded and causal on
is the uncertainty, which is assumed to have a diagonal block structure whose elements are bounded and causal on 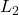
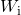 and
and 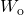 are frequency dependent weighting functions that describe the nature of the external disturbances and performance specifications respectively. In the remainder of this user manual, these are tacitly assumed to be merged in the plant
are frequency dependent weighting functions that describe the nature of the external disturbances and performance specifications respectively. In the remainder of this user manual, these are tacitly assumed to be merged in the plant 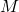 .
.

 structure
structureThe aim of the IQC analysis tool is to verify whether the (weighted) interconnection of ![]() is stable for all modelled uncertainties from a given set
is stable for all modelled uncertainties from a given set ![]() with
with ![]() , while, optionally, a certain performance metric on the performance channel is satisfied.
, while, optionally, a certain performance metric on the performance channel is satisfied.
The plant ![]() can have a multitude of in- and output channels that can be classified as uncertainty or performance channel. Here we emphasize that:
can have a multitude of in- and output channels that can be classified as uncertainty or performance channel. Here we emphasize that:
- it is not relevant in which order the performance and/or uncertainty channels are defined (as long as each block is associated with the proper channels of
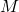 );
); - uncertainty blocks can be easily combined;
- channels may be left unassigned, which just means that they will not be taken into account in the analysis.
- both continuous- as well as discrete time systems may be considered.
