ultv: LTV parametric uncertainties

The class ultv is defined by LTV parametric uncertainties of the form:

$\Delta_\mathrm{ultv}(\delta)=\sum_{i=1}^{N}\delta_iT_i= \delta_1T_1+\cdots+ \delta_NT_N.$

Here

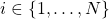$T_i$ , $i\in\{1,\ldots,N\}$ are fixed matrices $T_i\in\mathbb{R}^{n\times m}$ (having the same size as $\Delta_\mathrm{ultv}$ ).
$\delta:[0,\infty]\rightarrow\Lambda$ is a piecewise continuous time-varying parameter vector that takes its values form the (compact) polytope
$\Lambda=\mathrm{co}\{\delta^1,\ldots,\delta^M\}=\left\{\sum_{a=1}^{M}b_a\delta^a: b_a\geq0,\ \sum_{a=1}^{M}b_a=1\right\}$
with $\delta^a=(\delta_1^a,\ldots,\delta_N^a)$ , $a\in\{1,\ldots,M\}$ as generator points.
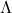$\Lambda$ is assumed to be star convex: $[0,1]\Lambda\subset\Lambda$

The ultis class can be defined by

$\Delta_\mathrm{ultv}=ultv('name')$
$\Delta_\mathrm{ultv}=ultv('name',varargin)$

Just specifying $\Delta_\mathrm{ultv}=ultv('name')$ defines an LTV parametric uncertainty $\delta$ on the interval $[-1,1]$ , which is repeated once (i.e., $\Delta_\mathrm{ultv}(\delta)=\delta_1\in[-1,1]$ and $T_1=1$ ).

Specifying and/or changing properties proceeds as summarized in the following two tables for properties related to the uncertainty and to IQC-multiplier respectively.

\[\left[\begin{array}{ccc}\delta_1^{p_1}&\cdots& \delta_N^{p_1}\\\vdots& \cdots& \vdots\\ \delta_1^{p_M}&\cdots& \delta_N^{p_M}\end{array}\right]\] — Uncertainty characteristics

Property	Description
RelaxationType	Specify the relaxation type. Options are (default = ‘DG’): – DG-scalings: ‘DG’ – Convex hull relaxation: ‘CH’ – Partial convexity: ‘PC’ – Zeroth order Polya relaxation: ‘ZP’
PrimalDual	Specify whether the multiplier should be a primal/dual parametrization (default = ‘Primal’). – Primal multipliers: ‘Primal’ – Dual multipliers: ‘Dual’ Note: For a standard IQC-analysis, all multipliers must be primal ones.

Multiplier characteristics

Note: See Section 5.2 of [1] for the details on the mathematical derivation of the IQC-multiplier.

Property	Description
Polytope	With the option Polytope on can specify the generator points of $\Delta_\mathrm{ultv}$ as $\left[\begin{array}{ccc}\delta_1^{p_1}&\cdots& \delta_N^{p_1}\\\vdots& \cdots& \vdots\\ \delta_1^{p_M}&\cdots& \delta_N^{p_M}\end{array}\right]$ Note: It is always assumed that the 0 is contained in the set.
UncertaintyMap	Specify the matrices $T_1,\ldots,T_N$ as a cell array $T=\{T_1,\ldots,T_N\}$ . This defines the uncertainty map $\Delta_\mathrm{ultv}(\delta)=\delta_1T_1+\cdots+ \delta_NT_N$ . Note: In case you wish to apply the DG-relaxation scheme, $T_1,\ldots,T_N$ must be defined such that $\Delta_\mathrm{ultv}(\delta)=\mathrm{diag}(\delta_1I_{\delta_1},\ldots, \delta_N <em>I_{\delta_N</em>})$ with $\delta_i\in[-1,1]$ , $i\in\{1,\ldots,N\}$ begin normalized.
InputChannel/ OutputChannel	Specify which input and output channels of the uncertain plant are affected by $\Delta_\mathrm{ultv}$ . For each $\delta_i$ , the channels should be specified as: $\begin{array}{c} row_{in,i}=\left[\begin{array}{ccc}C_{x_i}^{in}&\cdots&C_{y_i}^{in}\end{array}\right]\\row_{out,i}=\left[\begin{array}{ccc}C_{v_i}^{in}&\cdots&C_{w_i}^{in}\end{array}\right] \end{array}$ Here the order of the channels is not relevant, while $C_{m_i}^{in}$ , $C_{n_i}^{out}$ respectively denote the $m^{th}$ and $n^{th}$ in- and output channel of the uncertain plant $M$ . Note here thatthe row length of $row_{in,i}$ and $row_{out,i}$ equals the number of repetitions of $\delta_i$ . The option InputChannel/ OutputChannel should then be specified as a cell: $\begin{array}{c}InputChannel= \\ =\left\{\!\!\!\begin{array}{ccc}row_{in,1}\!\!\!&\cdots\!\!\!& row_{in,N} \end{array}\!\!\!\right\}\\OutputChannel =\\ =\left\{\!\!\!\begin{array}{ccc} row_{out,1}\!\!\!\!&\cdots\!\!\!\!&row_{ out ,N} \end{array}\!\!\!\right\}\end{array}$