fSmooth – IQClab

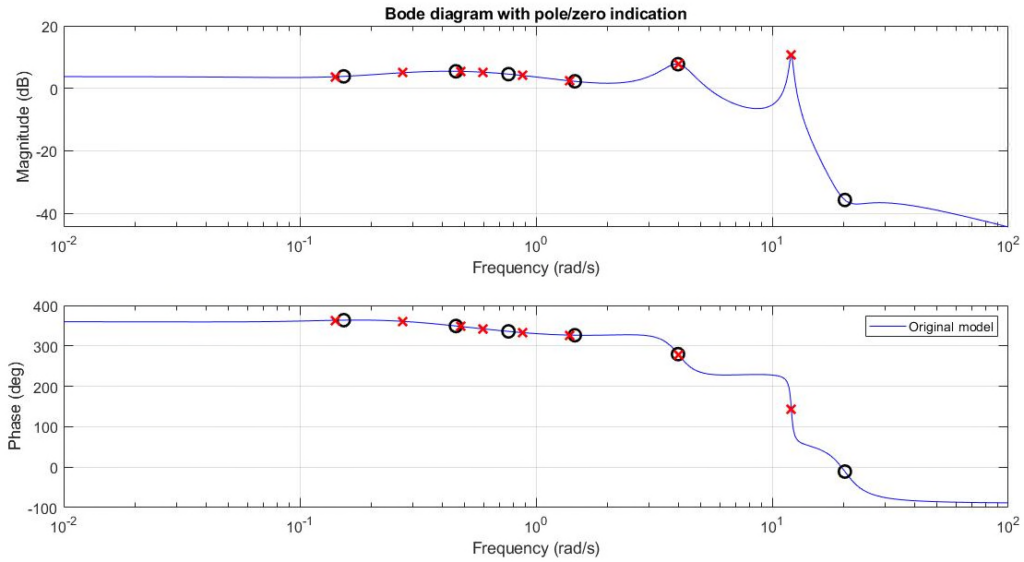
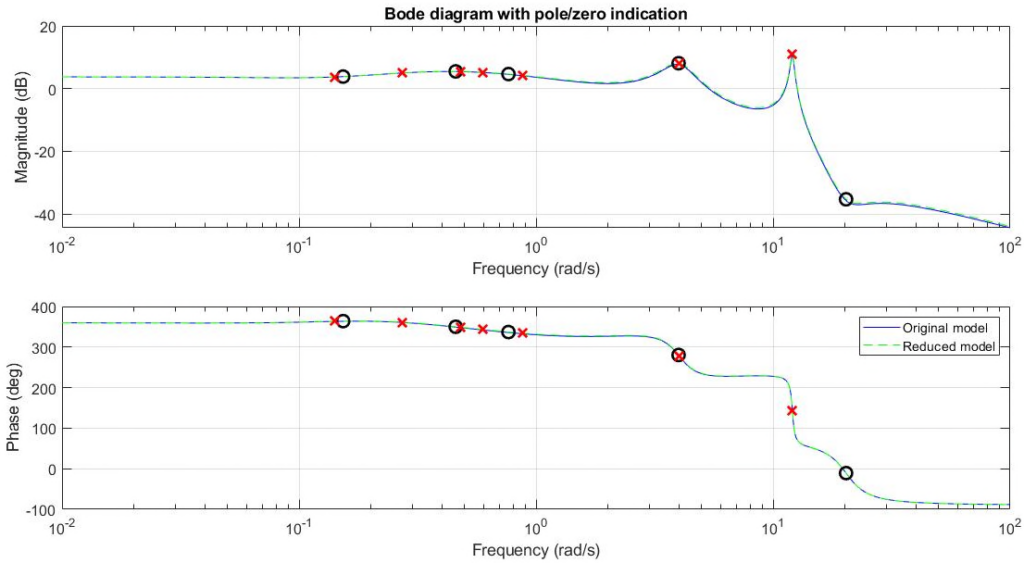
Similar to fRFZP, the function fSmooth allows smoothening a given model within a pre-specified frequency band by removing all poles and zeros within the specified range. This function is useful, for example, to remove near pole-zero cancellations (but which are too far from one-another to be removed using minreal).

The operation proceeds by specifying $G_\mathrm{red}=fSmooth(G,\omega)$ , where $G$ is the original model and $\omega$ is a $1\times 3$ vector, where the first two entries, $\omega_1$ and $\omega_2$ respectively, specify the frequency band in which the poles and zeros have to be removed, while the third entry, $\omega_3$ specifies the frequency at which the reduced order model should match its gain with the original system (i,e, $G_ \mathrm{red}(i\omega_3)= G(i\omega_3)$ ).

Example

The following code generates a random LTI SISO state space model with 10 states. Subsequently the function fBodePZ (see details) plots the corresponding Bode diagram together with the poles and zeros of the model. This is shown in the first plot below. The user is then asked to specify the frequency interval in which the poles and zeros should be removed. With $\omega_1=1$ , $\omega_2=2$ , and $\omega_3=10$ this yields the reduced order model shown in second figure below, where all poles and zeros between $\omega_1=1$ and $\omega_2=2$ have been removed.

G = rss(10,1,1);
w = logspace(-2,2,1000);
fignr = 1;
fBodePZ(w,fignr,G,’b-‘,’Original model’);
Gred = fSmooth(G);
close(1)
fBodePZ(w,fignr,Gred,’g–‘,’Reduced model’,G,’b-‘,’Original model’);