In this section it is demonstrated how to create an LTV parametric diagonally repeated and rate-bounded uncertainty block. To do so, suppose that this uncertainty has the following properties:
- name: ‘delta’
- Uncertainty block consisting of two parametric uncertainties
 and
and 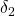
- bounds:
![Rendered by QuickLaTeX.com \delta_1\in[-1,1]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-6df548fdeecebbca619752484cf9738e_l3.png?media=1702023987) ,
, ![Rendered by QuickLaTeX.com \delta_2\in[-1,1]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-d77e46ebba1eba28f4cd385696b71327_l3.png?media=1702023987)
- rate- bounds:
![Rendered by QuickLaTeX.com \dot{\delta}_1\in[-0.1,0.1]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-70d20319927067ac9b17a922df14f77e_l3.png?media=1702023987) ,
, ![Rendered by QuickLaTeX.com \dot{\delta}_2\in[-0.5,0.5]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-ab33ee7dbbac0dddab0117cdbcbee666_l3.png?media=1702023987)
- number of repetitions: 2 and 3 times for
 and
and 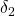 respectively
respectively - Input channels of
 connecting the uncertainty block:
connecting the uncertainty block: 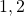 for
for  and
and 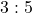 for the
for the 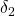
- Outputs channels of
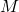 connecting the uncertainty block:
connecting the uncertainty block: 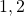 for
for  and
and 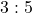 for
for 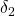
- This uncertainty can be created as follows:
delta = iqcdelta('delta','TimeInvTimeVar','TV','InputChannel',{[1:2],[3:5]},'OutputChannel',{[1:2],[3:5]},'Bounds',{[-1,1],[-1,1]},'RateBounds',{[-0.1,0.1],[-0.5,0.5]});
Alternatively, though in a bit more cumbersome way, you can also specify each block independently and then combine them with blkdiag as follows:
delta1 = iqcdelta('delta1','TimeInvTimeVar','TV','InputChannel',1:2,'OutputChannel',1:2,'Bounds',[-1,1],'RateBounds',[-0.1,0.1]);
delta2 = iqcdelta('delta2','TimeInvTimeVar','TV','InputChannel',3:5,'OutputChannel',3:5,'Bounds',[-1,1],'RateBounds',[-0.5,0.5]);
delta = blkdiag('delta',delta1,delta2);
In a next step, you have to assign an IQC-multiplier. The appropriate class for this is called ultv_rb (for details see here).
For this multiplier you have to choose the properties related to the basis function as well as the type of relaxation. For example, let us choose:
- Length: 3 (this corresponds to a McMillan degree of 2)
- Pole location: -1
- Relaxation type: ‘DG’
delta = iqcassign(delta,'ultv_rb','Length',3,'PoleLocation',-1,'RelaxationType','DG');
