The function ![]() creates minimum state space realizations for various basis functions that are used for the parametrization of IQC-multipliers. Here
creates minimum state space realizations for various basis functions that are used for the parametrization of IQC-multipliers. Here
 is the length of the basis function, which equals the McMillan degree
is the length of the basis function, which equals the McMillan degree 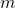 plus 1 (i.e.,
plus 1 (i.e., 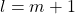 ).
).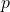 is the pole location of the basis function.
is the pole location of the basis function.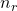 is the number of diagonal repetitions of the basis function
is the number of diagonal repetitions of the basis function is the type of basis function. The current version includes 4 versions as specified next:
is the type of basis function. The current version includes 4 versions as specified next:
| Type | Description |
| |
| |
| |
| This is the complex conjugate of | |
| This is the discrete time version of | |
| This is the discrete time version of | |
| This is the discrete time version of |

![Rendered by QuickLaTeX.com \[\psi=\left(\begin{array}{c}1\\\frac{(i\omega+pl)}{(i\omega-pl)}\\ \frac{(i\omega+pl)^2}{ (i\omega-pl)^2}\\\vdots\\ \frac{(i\omega+pl)^l}{ (i\omega-pl)^l} \end{array}\right)\otimes I_{n_r}\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-35cfd39e40bb91e9c4801f6303c7b530_l3.png?media=1702023987)
![Rendered by QuickLaTeX.com \[\psi=\left(\begin{array}{c}1\\ \frac{(i\omega)}{(i\omega-pl)^{l-1}}\\ \vdots\\\frac{(i\omega)^{l-1}}{(i\omega-pl)^{l-1}}\end{array}\right)\otimes I_{n_r}\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-e76273e00b2c0a6749f2b32abb1bf5ab_l3.png?media=1702023987)
![Rendered by QuickLaTeX.com \[\psi=\left(\begin{array}{c}1\\\frac{1}{(i\omega-pl)}\\ \frac{1}{ (i\omega-pl)^2}\\\vdots\\ \frac{1}{(i\omega-pl)^l}\end{array}\right)\otimes I_{n_r}\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-15da8809c52d90e3163b41899786a41f_l3.png?media=1702023987)