The function ![]() extends the plant
extends the plant ![]() to
to ![]() by adding new outputs to the plant in the following sense.
by adding new outputs to the plant in the following sense.
Given the original plant ![]() with realization
with realization
![Rendered by QuickLaTeX.com \left(\!\!\begin{array}{cccc}M_{11}&M_{12}&\cdots&M_{1n}\\ M_{21}&M_{22}&\cdots&M_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ M_{m1}&M_{m2}&\cdots&M_{mn}\end{array} \!\! \right)\!=\!\left[ \!\! \begin{array}{c|cccc}A&B_1&B_2&\cdots&B_n\\ \hline C_1&D_{11}&D_{12}&\cdots&D_{1n}\\C_2& D_{21}&D_{22}&\cdots&D_{2n}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ C_{m}&D_{m1}&D_{m2}&\cdots&D_{mn}\end{array}\!\!\right]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-d03cd31f6b84468a82afc4a10962dfea_l3.png?media=1702023987)
the function creates the extended plant ![]() with realization
with realization
![Rendered by QuickLaTeX.com \left(\!\!\begin{array}{cccc}M_{11}&M_{12}&\cdots&M_{1n}\\I&0&\cdots&0\\ M_{21}&M_{22}&\cdots&M_{2n}\\ 0&I&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ \vdots&\vdots&\ddots&\vdots\\ M_{m1}&M_{m2}&\cdots&M_{mn}\\0&0&\cdots&I\end{array}\!\!\right)\!=\!\left[ \!\! \begin{array}{c|cccc}A&B_1&B_2&\cdots&B_n\\ \hline C_1&D_{11}&D_{12}&\cdots&D_{1n}\\0&I&0&\cdots&0\\C_2& D_{21}&D_{22}&\cdots&D_{2n}\\ 0&0&I&\cdots&0\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ C_{m}&D_{m1}&D_{m2}&\cdots&D_{mn}\\ 0&0&0&\cdots&I\end{array}\!\!\right]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-8798a6a4f3d49e59a6530536decd9420_l3.png?media=1702023987)
If the option options.pd=’dual_augm’ is specified (default: options.pd=’primal_augm’), then the conjugate system (i.e., ![]() )
)
![Rendered by QuickLaTeX.com \left(\!\!\begin{array}{cccc}-M_{11}^T& -M_{21}^T&\cdots&-M_{m1}^T\\ -M_{12}^T&-M_{22}^T&\cdots&-M_{m2}^T\\ \vdots&\vdots&\ddots&\vdots\\ -M_{1n}^T&-M_{2m}^T &\cdots&-M_{mn}^T\end{array} \!\! \right)\!=\!\left[ \!\! \begin{array}{c|cccc}-A^T&-C_1^T&-C_2^T&\cdots&C_m^T\\ \hline -B_1^T&-D_{11}^T&-D_{21}^T&\cdots&-D_{m1}^T\\-B_2^T&-D_{12}^T&-D_{22}^T&\cdots&-D_{m2}^T\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ -B_{n}^T &-D_{1n}^T &-D_{2n}^T& \cdots&-D_{mn}^T\end{array}\!\!\right]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-5f51d6d7389b3a1ad64ada5fac977367_l3.png?media=1702023987)
is extended as
![Rendered by QuickLaTeX.com \left(\!\!\begin{array}{cccc}I&0&\cdots&0\\-M_{11}^T& -M_{21}^T&\cdots&-M_{m1}^T\\0&I&\cdots&0\\ -M_{12}^T&-M_{22}^T&\cdots&-M_{m2}^T\\ \vdots&\vdots&\ddots&\vdots\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&I\\ -M_{1n}^T&-M_{2m}^T &\cdots&-M_{mn}^T\end{array} \!\! \right)\!=\!\left[ \!\! \begin{array}{c|cccc}-A^T&-C_1^T&-C_2^T&\cdots&C_m^T\\ \hline 0&I&0&\cdots&0\\-B_1^T&-D_{11}^T&-D_{21}^T&\cdots&-D_{m1}^T\\0&0&I&\cdots&0\\-B_2^T&-D_{12}^T&-D_{22}^T&\cdots&-D_{m2}^T\\ \vdots&\vdots&\vdots&\ddots&\vdots \\ \vdots&\vdots&\vdots&\ddots&\vdots \\0&0&0&\cdots&I\\ -B_{n}^T &-D_{1n}^T &-D_{2n}^T& \cdots&-D_{mn}^T\end{array}\!\!\right]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-ec7c0f6dd8e44c99750ff747f8d01c93_l3.png?media=1702023987)
The second input of the function specifies where the identity matrices should be added. This can be done by specifying the structure io, which is a structure that is automatically generated by the method in the class iqcprob that is called when generating IQC multipliers for the uncertain plant ![]() .
.
To explain this in more detail, when creating IQC multipliers in IQClab, they are factorized as:
![]()
 is a symmetric matrix with LMI variables
is a symmetric matrix with LMI variables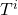 is an upper triangular scaling matrix
is an upper triangular scaling matrix is a basis (transfer) function
is a basis (transfer) function
This allows to construct the analysis FDI
![Rendered by QuickLaTeX.com \[\left(\bullet\right)^*\left(\!\!\begin{array}{c|c|c|c}\Pi^1&0&\cdots&0\\ \hline 0&\Pi^2&\ddots&\vdots\\ \hline \vdots&\ddots &\ddots &0\\ \hline 0&\cdots &0&\Pi_m\end{array}\!\!\right)\!\! \left(\!\!\begin{array}{cccc}M_{11}&M_{12}&\cdots&M_{1n}\\I&0&\cdots&0\\ \hline M_{21}&M_{22}&\cdots&M_{2n}\\ 0&I&\cdots&0\\ \hline\vdots&\vdots&\ddots&\vdots\\ \vdots&\vdots&\ddots&\vdots\\ M_{m1}&M_{m2}&\cdots&M_{mn}\\0&0&\cdots&I\end{array}\!\!\right)\prec0\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-5a760706d3fe8aad27dc66bd97e1f468_l3.png?media=1702023987)
An IQC problem is created by means of the problem class iqcprob. This class includes the method fIO, which stores the dimensions of these matrices in the row vector as![]()
Here:
 denotes the number of outputs of the uncertainty block
denotes the number of outputs of the uncertainty block denotes the number of inputs of the uncertainty block
denotes the number of inputs of the uncertainty block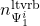 denotes the number of outputs of the uncertainty block in case of LTV rate bounded multipliers
denotes the number of outputs of the uncertainty block in case of LTV rate bounded multipliers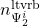 denotes the number of inputs of the uncertainty block in case of LTV rate bounded multipliers
denotes the number of inputs of the uncertainty block in case of LTV rate bounded multipliers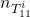 denotes the number of columns of
denotes the number of columns of 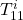
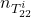 denotes the number of columns of
denotes the number of columns of 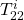
 denotes the number of columns of
denotes the number of columns of 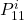
 denotes the number of columns of
denotes the number of columns of 
 denotes the number of states of
denotes the number of states of 
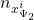 denotes the number of states of
denotes the number of states of 
The dimension of the identity blocks in the extended plant, ![]() , correspond to the dimensions of the uncertainty block (i.e.,
, correspond to the dimensions of the uncertainty block (i.e., ![]() ,
, ![]() and
and ![]() ,
, ![]() in case of the multiplier class for LTV rate-bounded uncertainties). Hence, the size of the identity block equals
in case of the multiplier class for LTV rate-bounded uncertainties). Hence, the size of the identity block equals ![]() .
.
Notes:
- In case the option options.n is specified, with
![Rendered by QuickLaTeX.com n=[n_1,n_2]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-04d2e44007ada9f89586bfc48f2b1423_l3.png?media=1702023987) , you define the start and stop criteria such that the code starts at
, you define the start and stop criteria such that the code starts at  and ends at
and ends at 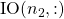 .
. - In case of of the multiplier class for LTV rate-bounded uncertainties, the plant
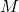 is extended with an extra identity block as follows:
is extended with an extra identity block as follows: ![Rendered by QuickLaTeX.com \[\left(\begin{array}{cc}\Psi_{1}^i&0\\0&\Psi_{2}^i\end{array}\right)\left(\begin{array}{cc}M^i&0\\I&0\\0&I\end{array}\right)\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-3c059455f9a0903443b36125fae60838_l3.png?media=1702023987)
- The function can also be applied independently from the problem class iqcprob, just by providing the proper inputs to the function.
