The function ![]() constructs the extended full-block multiplier
constructs the extended full-block multiplier
![]()
 with
with  and
and 
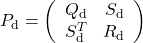 with
with  and
and 
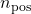 denotes the number of positive eigenvalues of
denotes the number of positive eigenvalues of  (this equals the size of
(this equals the size of  )
)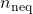 denotes the number of negative eigenvalues of
denotes the number of negative eigenvalues of  (this equals the size of
(this equals the size of  )
) specifies the type of extention:
specifies the type of extention: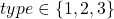 :
:
is such that![Rendered by QuickLaTeX.com \[P_\mathrm{e}=\left(\begin{array}{cc}Q_\mathrm{e}&S_\mathrm{e}\\ S_\mathrm{e}^T&R_\mathrm{e}\end{array}\right)\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-795a63c78c86d7e88810ca6745580446_l3.png?media=1702023987)
![Rendered by QuickLaTeX.com \[P_\mathrm{e}^{-1}=\left(\begin{array}{cccc}Q_\mathrm{e}&\star&S_\mathrm{e}&\star\\ \star&\star&\star&\star\\ S_\mathrm{e}^T&\star&R_\mathrm{e}&\star\\ \star&\star&\star&\star\end{array}\right)\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-f062d436da5694faef2f32d605ed0f2b_l3.png?media=1702023987)
 :
:
is such that![Rendered by QuickLaTeX.com \[P_\mathrm{e}=\left(\begin{array}{cc}Q_\mathrm{d}&S_\mathrm{d}\\ S_\mathrm{d}^T&R_\mathrm{d}\end{array}\right)\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-8a1e49ffd7a4b84e2b5d37105243f1df_l3.png?media=1702023987)
with![Rendered by QuickLaTeX.com \[P_\mathrm{e}^{-1}=\left(\begin{array}{cccc}Q_\mathrm{di}&\star&S_\mathrm{di}&\star\\ \star&\star&\star&\star\\ S_\mathrm{di}^T&\star&R_\mathrm{di}&\star\\ \star&\star&\star&\star\end{array}\right)\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-4f0a42e075135cc993fe8e94b396cbb3_l3.png?media=1702023987)
![Rendered by QuickLaTeX.com \[P_\mathrm{d}^{-1}=\left(\begin{array}{cc}Q_\mathrm{d}&S_\mathrm{d}\\ S_\mathrm{d}^T&R_\mathrm{d}\end{array}\right)^{-1}=\left(\begin{array}{cc}Q_\mathrm{di}&S_\mathrm{di}\\ S_\mathrm{di}^T&R_\mathrm{di}\end{array}\right)\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-b3e4f499ad552e144b67841a992fcd6a_l3.png?media=1702023987)
Let ![]() and
and ![]() . Then the different types are defined as follows:
. Then the different types are defined as follows:
| Type | Description |
| type=1 | Define Then |
| type=2 | Define Then |
| type=3 | – Factorize – Define – Let Then |
| type=4 | Define Then |
| type=5 | Define Then |
| type=6 | – Factorize – Define – Let Then |
