The function ![]() factorizes the symmetric (or Hermitian)
factorizes the symmetric (or Hermitian) ![]() matrix as:
matrix as:
![Rendered by QuickLaTeX.com \[P=M^TJM=M^T\left(\begin{array}{ccc}I_{n_+}&0&0\\0&0_{n_0}&0\\0&0& I_{n_-} \end{array}\right)M\]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-e40c60c6e1e3464ce4f7f7dde0abe948_l3.png?media=1702023987)
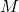 is the outer factor
is the outer factor is the middle term
is the middle term is the set of eigenvectors of P
is the set of eigenvectors of P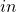 is the vector
is the vector ![Rendered by QuickLaTeX.com in=[n_+,n_0,n_-]](https://usercontent.one/wp/www.iqclab.eu/wp-content/ql-cache/quicklatex.com-59e4dba43bd17f502f177a8449c93664_l3.png?media=1702023987) , where
, where 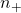 ,
, 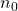 , and
, and  are the number of positive, zero, and negative eigenvalues respectively.
are the number of positive, zero, and negative eigenvalues respectively.
